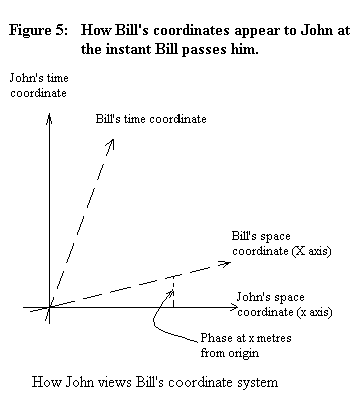Special Relativity/Simultaneity, time dilation and length contraction

More about the relativity of simultaneity and the Andromeda paradox

If two observers who are moving relative to each other synchronise their clocks in their own frames of reference they discover that the clocks do not agree between the reference frames. This is illustrated below:

The effect of the relativity of simultaneity, or "phase", is for each observer to consider that a different set of events is simultaneous. Phase means that observers who are moving relative to each other have different sets of things that are simultaneous, or in their "present moment".

The amount by which the clocks differ between two observers depends upon the distance of the clock from the observer ($t=xv/c^2$). Notice that if both observers are part of inertial frames of reference with clocks that are synchronised at every point in space then the phase difference can be obtained by simply reading the difference between the clocks at the distant point and clocks at the origin. This difference will have the same value for both observers.

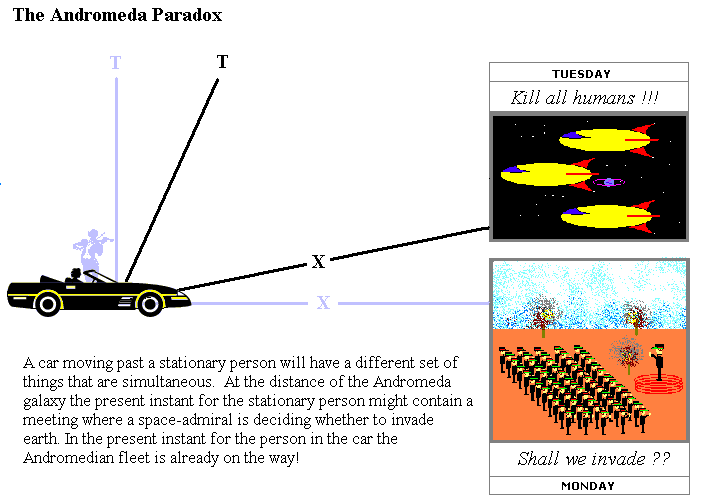
Relativistic phase differences have the startling consequence that at distances as large as our separation from nearby galaxies an observer who is driving on the earth can have a radically different set of events in her "present moment" from another person who is standing on the earth. The classic example of this effect of phase is the "Andromeda Paradox", also known as the "Rietdijk-Putnam-Penrose" argument. Penrose described the argument:

"Two people pass each other on the street; and according to one of the two people, an Andromedean space fleet has already set off on its journey, while to the other, the decision as to whether or not the journey will actually take place has not yet been made. How can there still be some uncertainty as to the outcome of that decision? If to either person the decision has already been made, then surely there cannot be any uncertainty. The launching of the space fleet is an inevitability." (Penrose 1989).

The argument is illustrated below:

This "paradox" has generated considerable philosophical debate on the nature of time and free-will. The advanced text of this book provides a discussion of some of the issues surrounding this geometrical interpretation of special relativity.

A result of the relativity of simultaneity is that if the car driver launches a space rocket towards the Andromeda galaxy it might have a several days head start compared with a space rocket launched from the ground. This is because the "present moment" for the moving car driver is progressively advanced with distance compared with the present moment on the ground. The present moment for the car driver is shown in the illustration below:

The result of the Andromeda paradox is that when someone is moving towards a distant point there are later events at that point than for someone who is not moving towards the distant point. There is a time gap between the events in the present moment of the two people.

The nature of length contraction

According to special relativity items such as measuring rods consist of events distributed in space and time. This means that two observers moving relative to each other will usually be observing measuring rods that are composed of different sets of events. If the word "rod" means the three dimensional form of the object called a rod then these two observers in relative motion observe different rods. Each observer has a different rod in their present moment. The way that observers observe different sets of events is shown in the illustration below:

File:Relrod.GIF

Each three dimensional section of the world is those events that are at an observer's present instant or present moment. The area of a Minkowski diagram that corresponds to all of the events that compose an object over a period of time is known as the worldtube of the object. It can be seen in the image below that length contraction is the result of observer's having different sections of an object's worldtube in their present instant.

(It should be recalled that the longest lengths on space-time diagrams are often the shortest in reality).

It is sometimes said that length contraction occurs because objects rotate into the time axis. This is actually a half truth, there is no actual rotation of a three dimensional rod, instead the observed three dimensional slice of a four dimensional rod is changed which makes it appear as if the rod has rotated into the time axis. In special relativity it is not the rod that rotates into time, it is the observer's slice of the worldtube of the rod that rotates.

There can be no doubt that the three dimensional slice of the worldtube of a rod does indeed have different lengths for relatively moving observers so that the relativistic contraction of the rod is a real, physical phenomenon.

The issue of whether or not the events that compose the worldtube of the rod are always existent is a matter for philosophical speculation.

Further reading: Vesselin Petkov. (2005) Is There an Alternative to the Block Universe View?

Evidence for length contraction, the field of an infinite straight current

Length contraction can be directly observed in the field of an infinitely straight current. This is shown in the illustration below.

Non-relativistic electromagnetism describes the electric field due to a charge using:

$E=\frac{\lambda }{2\pi {ϵ}_{0}r}$

and describes the magnetic field due to an infinitely long straight current using the Biot Savart law:

$B=\frac{{\mu }_{0}I}{2\pi r}$

Or using the charge density (from $I=\lambda v$ where $\lambda$ ):

$B=\frac{{\mu }_0\lambda v}{2\pi r}$

Using relativity it is possible to show that the formula for the magnetic field given above can be derived using the relativistic effect of length contraction on the electric field and so what we call the "magnetic" field can be understood as relativistic observations of a single phenomenon. The relativistic calculation is given below.

If Jim is moving relative to the wire at the same velocity as the negative charges he sees the wire contracted relative to Bill:

$l_{+}=l\sqrt{1-v^2/c^2}$

Bill should see the space between the charges that are moving along the wire to be contracted by the same amount but the requirement for electrical neutrality means that the moving charges will be spread out to match those in the frame of the fixed charges in the wire.

This means that Jim sees the negative charges spread out so that:

$l_{-}=\frac{l}{\sqrt{1-v^2/c^2}}$

The net charge density observed by Jim is:

$\lambda =\frac{q}{l_{-}}-\frac{q}{l_{+}}$

Substituting:

$\lambda =\frac{q}{l}(\sqrt{1-v^2/c^2}-\frac{1}{\sqrt{1-v^2/c^2}})$

Using the binomial expansion:

$\lambda =\frac{q}{l}(1-\frac{v^2}{2c^2}-1-\frac{v^2}{2c^2})$

Therefore, allowing for a net positive charge, the positive charges being fixed:

$\lambda =\frac{q{v}^2}{l{c}^2}$

The electric field at Jim's position is given by:

$E=\frac{\lambda v^2}{2\pi {ϵ}_{0}r{c}^2}$

The force due to the electrical field at Jim's position is given by $F=Eq$ which is:

$F=\frac{q\lambda v^2}{2\pi {ϵ}_{0}r{c}^2}$

Now, from classical electromagnetism:

$c^2=\frac{1}{{ϵ}_0{\mu }_0}$

So substituting this into $F=\frac{q\lambda v^2}{2\pi {ϵ}_{0}r{c}^2}$:

(1) $F=\frac{q{\mu }_0\lambda v^2}{2\pi r}$

This is the formula for the relativistic electric force that is observed by Bill as a magnetic force. How does this compare with the non-relativistic calculation of the magnetic force? The force on a charge at Jim's position due to the magnetic field is, from the classical formula:

$F=Bqv$

Which from the Biot-Savart law is:

(2) $F=\frac{q{\mu }_0\lambda v^2}{2\pi r}$

which shows that the same formula applies for the relativistic excess electrical force experienced by Jim as the formula for the classical magnetic force.

It can be seen that once the idea of space-time is understood the unification of the two fields is straightforward. Jim is moving relative to the wire at the same speed as the negatively charged current carriers so Jim only experiences an electric field. Bill is stationary relative to the wire and observes that the charges in the wire are balanced whereas Jim observes an imbalance of charge. Bill assigns the attraction between Jim and the current carriers to a "magnetic field".

It is important to notice that, in common with the explanation of length contraction given above, the events that constitute the stream of negative charges for Jim are not the same events as constitute the stream of negative charges for Bill. Bill and Jim's negative charges occupy different moments in time.

Incidently, the drift velocity of electrons in a wire is about a millimetre per second but a huge charge is available in a wire (See link below).

Further reading:

Purcell, E. M. Electricity and Magnetism. Berkeley Physics Course. Vol. 2. 2nd ed. New York, NY: McGraw-Hill. 1984. ISBN: 0070049084.

Useful links:

http://hyperphysics.phy-astr.gsu.edu/hbase/electric/ohmmic.html

http://hyperphysics.phy-astr.gsu.edu/hbase/relativ/releng.html

De Broglie waves

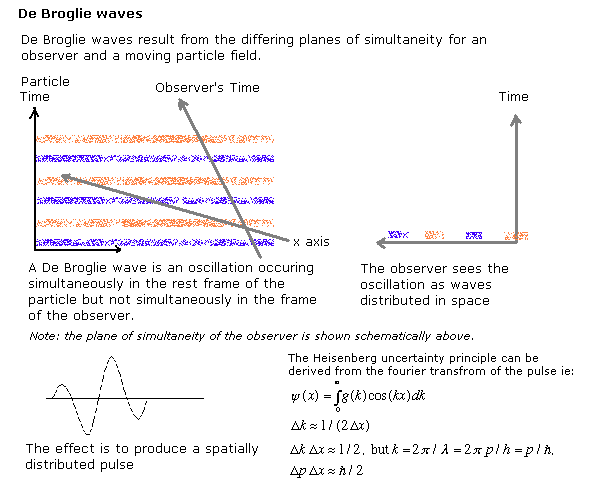
De Broglie noticed that the differing three dimensional sections of the universe would cause oscillations in the rest frame of an observer to appear as wave trains in the rest frame of observers who are moving.

He combined this insight with Einstein's ideas on the quantisation of energy to create the foundations of quantum theory. De Broglie's insight is also a round-about proof of the description of length contraction given above - observers in relative motion have differing three dimensional slices of a four dimensional universe. The existence of matter waves is direct experimental evidence of the relativity of simultaneity.

Further reading: de Broglie, L. (1925) On the theory of quanta. A translation of : RECHERCHES SUR LA THEORIE DES QUANTA (Ann. de Phys., 10e s´erie, t. III (Janvier-F ´evrier 1925).by: A. F. Kracklauer. http://www.ensmp.fr/aflb/LDB-oeuvres/De_Broglie_Kracklauer.pdf

Bell's spaceship paradox

Bell devised a thought experiment called the "Spaceship Paradox" to enquire whether length contraction involved a force and whether this contraction was a contraction of space. In the Spaceship Paradox two spaceships are connected by a thin, stiff string and are both equally and linearly accelerated to a velocity $v$ relative to the ground, at which, in the special relativity version of the paradox, the acceleration ceases. The acceleration on both spaceships is arranged to be equal according to ground observers so, according to observers on the ground, the spaceships will stay the same distance apart. It is asked whether the string would break.

It is useful when considering this problem to investigate what happens to a single spaceship. If a spaceship that has rear thrusters is accelerated linearly, according to ground observers, to a velocity $v$ then the ground observers will observe it to have contracted in the direction of motion. The acceleration experienced by the front of the spaceship will have been slightly less than the acceleration experienced by the rear of the spaceship during contraction and then would suddenly reach a high value, equalising the front and rear velocities, once the rear acceleration and increasing contraction had ceased. From the ground it would be observed that overall the acceleration at the rear could be linear but the acceleration at the front would be non-linear.

In Bell's thought experiment both spaceships are artificially constrained to have constant acceleration, according to the ground observers, until the acceleration ceases. Sudden adjustments are not allowed. Furthermore no difference between the accelerations at the front and rear of the assembly are permitted so any tendency towards contraction would need to be borne as tension and extension in the string.

The most interesting part of the paradox is what happens to the space between the ships. From the ground the spaceships will stay the same distance apart (the experiment is arranged to achieve this) whilst according to observers on the spaceships they will appear to become increasingly separated. This implies that acceleration is not invariant between reference frames (see Part II) and the force applied to the spaceships will indeed be affected by the difference in separation of the ships observed by each frame.

The section on the nature of length contraction above shows that as the string changes velocity the observers on the ground observe a changing set of events that compose the string. These new events define a string that is shorter than the original. This means that the string will indeed attempt to contract as observed from the ground and will be drawn out under tension as observed from the spaceships. If the string were unable to bear the extension and tension in the moving frame or the tension in the rest frame it would break.

Another interesting aspect of Bell's Spaceship Paradox is that in the inertial frames of the ships, owing to the relativity of simultaneity, the lead spaceship will always be moving slightly faster than the rear spaceship so the spaceship-string system does not form a true inertial frame of reference until the acceleration ceases in the frames of reference of both ships. The asynchrony of the cessation of acceleration shows that the lead ship reaches the final velocity before the rear ship in the frame of reference of either ship. However, this time difference is very slight (less than the time taken for an influence to travel down the string at the speed of light $x/c>vx/c^2$).

It is necessary at this stage to give a warning about extrapolating special relativity into the domain of general relativity (GR). SR cannot be applied with confidence to accelerating systems which is why the comments above have been confined to qualitative observations.

Further reading

Bell, J. S. (1976). Speakable and unspeakable in quantum mechanics. Cambridge University Press 1987 ISBN 0-521-52338-9

Hsu, J-P and Suzuki, N. (2005) Extended Lorentz Transformations for Accelerated Frames and the Solution of the “Two-Spaceship Paradox” AAPPS Bulletin October 2005 p.17 http://www.aapps.org/archive/bulletin/vol15/15-5/15_5_p17p21%7F.pdf

Matsuda, T and Kinoshita, A (2004. A Paradox of Two Space Ships in Special Relativity. AAPPS Bulletin February 2004 p3. http://www.aapps.org/archive/bulletin/vol14/14_1/14_1_p03p07.pdf

More about time dilation

The term "time dilation" is applied to the way that observers who are moving relative to you record fewer clock ticks between events than you. In special relativity this is not due to properties of the clocks, it is due to shorter distances between events along an observer's path through spacetime. This can be seen most clearly by re-examining the Andromeda Paradox.

Suppose Bill passes Jim at high velocity on the way to Mars. Jim has previously synchronised the clocks on Mars with his Earth clocks but for Bill the Martian clocks read times well in advance of Jim's. This means that Bill has a head start because his present instant contains what Jim considers to be the Martian future. Jim observes that Bill travels through both space and time. However, Bill achieves this strange time travel by having what Jim considers to be the future of distant objects in his present moment. Bill is literally travelling into future parts of Jim's frame of reference.

In special relativity time dilation and length contraction are not material effects, they are physical effects due to travel within a four dimensional spacetime.

It is important for advanced students to be aware that special relativity and General Relativity differ about the nature of spacetime. General Relativity, in the form championed by Einstein, abolishes the idea of extended space and time and is what is known as a "relationalist" theory of physics. Special relativity, on the other hand, is a theory where extended spacetime is pre-eminent. The brilliant flowering of physical theory in the early twentieth century has tended to obscure this difference because, within a decade, special relativity had been subsumed within General Relativity. The interpretation of special relativity that is presented here should be learnt before advancing to more advanced interpretations.

The twin paradox

The effects of the relativity of simultaneity such as are seen in the "Andromeda paradox" are, in part, the origin of the "twin paradox". If you have not understood the Andromeda Paradox you will not understand the twin paradox because it will not be obvious that the twin who turns round has a head start. In the twin paradox there are twins, Bill and Jim. Jim is on Earth. Bill flies past Jim in a spaceship, goes to a distant point such as Mars, turns round and flies back again. It is found that Bill records fewer clock ticks over the whole journey than Jim records on earth. Why?

The twin paradox seems to cause students more problems than almost any other area of special relativity. Students sometimes reason that "all motion is relative" and time dilation applies so wonder why, if Jim sees Bill's clocks read 15 seconds for a journey, Bill doesn't reciprocally see Jim's clocks read only 9 seconds? This mistake arises for two reasons, firstly relativity does not hold that "all motion is relative", this is not a postulate of the theory, secondly Bill moves through space so the effects of the relativity of simultaneity must be considered as well as time dilation.

The analysis given below follows Bohm's approach (see "further reading" below). Suppose Jim has synchronised his clocks on Earth with those on Mars. As Bill flies past Jim he synchronises his clock with Jim's clock on Earth. When he does this he realises that the relativity of simultaneity applies and so, for Bill, the clocks on Mars are not synchronised with either his or Jim's clocks. To Bill it will appear that Jim has synchronised his clocks incorrectly. There is a time difference, or "gap", between Bill's clocks and those on Mars even when he passes Jim. This difference is equal to the relativistic phase at the distant point. This set of events is almost identical to the set of events that were discussed above in the Andromeda Paradox.

Bill flies to Mars and discovers that the clocks there are reading a later time than his own clock. He turns round to fly back to Earth and realises that the relativity of simultaneity means that the clocks on Earth will have jumped forward, yet another "time gap" appears. When Bill gets back to Earth the time gaps and time dilations mean that people on Earth have recorded more clock ticks that he did.

For ease of calculation suppose that Bill is moving at a truly astonishing velocity of 0.8c in the direction of a distant point that is 10 light seconds away (about 3 million kilometres). The illustration below shows Jim and Bill's observations:

From Bill's viewpoint there is both a time dilation and a phase effect. It is the added factor of "phase" that explains why, although the time dilation occurs for both observers, Bill observes the same readings on Jim's clocks over the whole journey as does Jim.

To summarise the mathematics of the twin paradox using the example:

Jim observes the distance as 10 light seconds and the distant point is in his frame of reference. According to Jim it takes Bill the following time to make the journey:

Time taken = distance / velocity therefore according to Jim:

$t=10/0.8=12.5$ seconds

Again according to Jim, time dilation should affect the observed time on Bill's clocks:

$T=t\times \sqrt{1-v^2/c^2}$ so:

$T=12.5\times \sqrt{1-0.8^2}=7.5$ seconds

So for Jim the round trip takes 25 secs and Bill's clock reads 15 secs.

Bill measures the distance as:

$X=x\times \sqrt{1-v^2/c^2}=10\times \sqrt{1-0.8^2}=6$ light seconds.

For Bill it takes $X/v=6/0.8=7.5$ seconds.

Bill observes Jim's clocks to appear to run slow as a result of time dilation:

$t^{\text{'}}=T\times \sqrt{1-v^2/c^2}$ so:

$t^{\text{'}}=7.5\times \sqrt{1-0.8^2}=4.5$ seconds

But there is also a time gap of $vx/c^2=8$ seconds.

So for Bill, Jim's clocks register 12.5 secs have passed from the start to the distant point. This is composed of 4.5 secs elapsing on Jim's clocks at the turn round point plus an 8 sec time gap from the start of the journey. Bill sees 25 secs total time recorded on Jim's clocks over the whole journey, this is the same time as Jim observes on his own clocks.

It is sometimes dubiously asserted that the twin paradox is about the clocks on the twin that leaves earth being slower than those on the twin that stays at home, it is then argued that biological processes contain clocks therefore the twin that travelled away ages less. This is not really true because the relativistic phase plays a major role in the twin paradox and leads to Bill travelling to a remote place that, for Bill, is at a later time than Jim when Bill and Jim pass each other. A more accurate explanation is that when we travel we travel in time as well as space.

The turn around is not required to demonstrate the twin "paradox". Suppose there were two travellers, Bill(1) who moves away from earth and Bill(2) who travels towards earth. If Bill(2) synchronises his clocks with the clocks on Bill(1) when they pass then the same difference in elapsed time between the clocks on Jim and Bill(2) will be observed as between Jim and Bill in the original example.

Students have difficulty with the twin paradox because they believe that the observations of the twins are symmetrical. This is not the case. As can be seen from the illustration below either twin could determine whether they had made the turn or the other twin had made the turn.

Jim and Bill's view of the journey

Special relativity does not postulate that all motion is 'relative'; the postulates are that the laws of physics are the same in all inertial frames and there is a constant velocity called the "speed of light". Contrary to popular myth the twins do not observe events that are a mirror image of each other. Bill observes himself leave Jim then return, Jim sees Bill leave him then return. Bill does not observe Jim turn round, he observes himself making the turn.

The following illustrations cover various views of the journey. The most important moment in the journey is the point where Bill turns round. Notice how Bill's surface of simultaneity, that includes the events that he considers to be in the present moment, swings across Jim's worldline during the turn.

As Bill travels away from Jim he considers events that are already in Jim's past to be in his own present.

After the turn Bill considers events that are in Jim's future to be in his present (although the finite speed of light prevents Bill from observing Jim's future).

The swing in Bill's surface of simultaneity at the turn-round point leads to a 'time gap'. In our example Bill might surmise that Jim's clocks jump by 16 seconds on the turn.

Notice that the term "Jim's apparent path" is used in the illustration - as was seen earlier, Bill knows that he himself has left Jim and returned so he knows that Jim's apparent path is an artefact of his own motion. If we imagine that the twin paradox is symmetrical then the illustration above shows how we might imagine Bill would view the journey. But what happens, in our example, to the 16 seconds in the time gap, does it just disappear? The twin paradox is not symmetrical and Jim does not make a sudden turn after 4.5 seconds. Bill's actual observation and the fate of the information in the time gap can be probed by supposing that Jim emits a pulse of light several times a second. The result is shown in the illustration below.

Jim has clearly but one inertial frame but does Bill represent a single inertial frame? Suppose Bill was on a planet as he passed Jim and flew back to Jim in a rocket from the turn-round point: how many inertial frames would be involved? Is Bill's view a view from a single inertial frame?

Exercise: it is interesting to calculate the observations made by an observer who continues in the direction of the outward leg of Bill's journey - note that a velocity transformation will be needed to estimate Bill's inbound velocity as measured by this third observer.

Further reading:

Bohm, D. The Special Theory of Relativity (W. A. Benjamin, 1965).

D’Inverno, R. Introducing Einstein’s Relativity (Oxford University Press, 1992).

Eagle, A. A note on Dolby and Gull on radar time and the twin "paradox". American Journal of Physics. 2005, VOL 73; NUMB 10, pages 976-978. http://arxiv.org/PS_cache/physics/pdf/0411/0411008v2.pdf

The Pole-barn paradox

(Note that Minkowski's metric involves the subtraction of displacements in time, so what appear to be the longest lengths on a 2D sheet of paper are often the shortest lengths in a (3+1)D reality).

The symmetry of length contraction leads to two questions. Firstly, how can a succession of events be observed as simultaneous events by another observer? This question led to the concept of de Broglie waves and quantum theory. Secondly, if a rod is simultaneously between two points in one frame how can it be observed as being successively between those points in another frame? For instance, if a pole enters a building at high speed how can one observer find it is fully within the building and another find that the two ends of the rod are opposed to the two ends of the building at successive times? What happens if the rod hits the end of the building? The second question is known as the "pole-barn paradox" or "ladder paradox".

The pole-barn paradox states the following: suppose a superhero running at 0.75c and carrying a horizontal pole 15 m long towards a barn 10m long, with front and rear doors. When the runner and the pole are inside the barn, a ground observer closes and then opens both doors (by remote control) so that the runner and pole are momentarily captured inside the barn and then proceed to exit the barn from the back door.

One may be surprised to see a 15-m pole fit inside a 10-m barn. But the pole is in motion with respect to the ground observer, who measures the pole to be contracted to a length of 9.9 m (check using equations).

The “paradox” arises when we consider the runner’s point of view. The runner sees the barn contracted to 6.6 m. Because the pole is in the rest frame of the runner, the runner measures it to have its proper length of 15 m. Now, how can our superhero make it safely through the barn?

The resolution of the “paradox” lies in the relativity of simultaneity. The closing of the two doors is measured to be simultaneous by the ground observer. However, since the doors are at different positions, the runner says that they do not close simultaneously. The rear door closes and then opens first, allowing the leading edge of the pole to exit. The front door of the barn does not close until the trailing edge of the pole passes by.

What happens if the rear door is kept closed and made out of some impenetrable material? Can we or can we not trap the rod inside the barn by closing the front door while the whole rod is inside according to a ground observer? When the front end of the rod hits the rear door, information about this impact will travel backwards along the rod in the form of a shock wave. The information cannot travel faster than c, so the rear end of the rod will continue to travel forward at its original speed until the wave reaches it. Even if the shock wave is traveling at the speed of light, it will not reach the rear end of the rod until after the rear end has passed through the front door even in the runner's frame. Therefore the whole rod (albeit quite scrunched up) will be inside the barn when the front door closes. If it is infinitely elastic, it will end up compressed and "spring loaded" against the inside of the closed barn.

The transverse doppler effect

The existence of time dilation means that the frequency of light emitted from a source that is moving towards or away from an observer should be red shifted in directions that are perpendicular to the direction of motion. The transverse doppler effect is given by:

$\nu ={\nu }^{\prime }\sqrt{1-\frac{v^2}{c^2}}$

Where $\nu$ is the observed frequency and ${\nu }^{\prime }$ is the frequency if the source were stationary relative to the observer (the proper frequency).

This effect was first confirmed by Ives and Stillwell in 1938. The transverse doppler effect is a purely relativistic effect and has been used as an example of proof that time dilation occurs.

Relativistic transformation of angles

If a rod makes an angle with its direction of motion toward or away from an observer the component of its length in the direction of motion will be contracted. This means that observed angles are also transformed during changes of frames of reference. Assuming that motion occurs along the x-axis, suppose the rod has a proper length (rest length) of $L^{\prime }$ metres and makes an angle of ${\theta }^{\prime }$degrees with the x'-axis in its rest frame. The tangent of the angle made with the axes is:

Tangent in rest frame of rod = $\tan {\theta }^{\prime }=\frac{L_y^{\prime }}{L_x^{\prime }}$

Tangent in observer's frame = $\tan \theta =\frac{L_y}{L_x}$

Therefore:

$\frac{\tan \theta }{\tan {\theta }^{\prime }}=\frac{L_y{L}_x^{\prime }}{L_y^{\prime }{L}_x}$

But $L_x=L_x^{\prime }\sqrt{1-v^2/c^2}$

And $L_y=L_y^{\prime }$

So

$\tan \theta =\frac{\tan {\theta }^{\prime }}{\sqrt{1-v^2/c^2}}$

Showing that angles with the direction of motion are observed to increase with velocity.

The angle made by a moving object with the x-axis also involves a transformation of velocities to calculate the correct angle of incidence.

Addition of velocities

How can two observers, moving at v km/sec relative to each other, compare their observations of the velocity of a third object?

Suppose one of the observers measures the velocity of the object as $u^{\text{'}}$ where:

$u^{\text{'}}=\frac{x^{\text{'}}}{t^{\text{'}}}$

The coordinates $x^{\text{'}}$ and $t^{\text{'}}$ are given by the Lorentz transformations:

$x^{\text{'}}=\frac{x-vt}{\sqrt{(1-v^2/c^2)}}$

and

$t^{\text{'}}=\frac{t-(v/c^2)x}{\sqrt{(1-v^2/c^2)}}$

but

$x^{\text{'}}=u^{\text{'}}{t}^{\text{'}}$

so:

$\frac{x-vt}{\sqrt{(1-v^2/c^2)}}=u^{\text{'}}\frac{t-(v/c^2)x}{\sqrt{(1-v^2/c^2)}}$

and hence:

$x-vt=u^{\text{'}}(t-vx/c^2)$

Notice the role of the phase term $vx/c^2$. The equation can be rearranged as:

$x=\frac{(u^{\text{'}}+v)}{(1+u^{\text{'}}v/c^2)}t$

given that $x=ut$:

$u=\frac{(u^{\text{'}}+v)}{(1+u^{\text{'}}v/c^2)}$

This is known as the relativistic velocity addition theorem, it applies to velocities parallel to the direction of mutual motion.

The existence of time dilation means that even when objects are moving perpendicular to the direction of motion there is a discrepancy between the velocities reported for an object by observers who are moving relative to each other. If there is any component of velocity in the x direction ($u_x$, ${u^{\text{'}}}_x$) then the phase affects time measurement and hence the velocities perpendicular to the x-axis. The table below summarises the relativistic addition of velocities in the various directions in space.

${u^{\text{'}}}_x=\frac{(u_x-v)}{(1-u_{x}v/c^2)}$	$u_x=\frac{({u^{\text{'}}}_x+v)}{(1+{u^{\text{'}}}_{x}v/c^2)}$
${u^{\text{'}}}_y=\frac{u_y\sqrt{1-v^2/c^2}}{(1-u_{x}v/c^2)}$	$u_y=\frac{{u^{\text{'}}}_y\sqrt{1-v^2/c^2}}{(1+{u^{\text{'}}}_{x}v/c^2)}$
${u^{\text{'}}}_z=\frac{u_z\sqrt{1-v^2/c^2}}{(1-u_{x}v/c^2)}$	$u_z=\frac{{u^{\text{'}}}_z\sqrt{1-v^2/c^2}}{(1+{u^{\text{'}}}_{x}v/c^2)}$

Notice that for an observer in another reference frame the sum of two velocities (u and v) can never exceed the speed of light. This means that the speed of light is the maximum velocity in any frame of reference.