How To Build a Pinewood Derby Car/Physics

This module has some simple physics and, at the end, some chemistry of the pinewood derby. A pinewood derby car converts gravitational potential energy to translational kinetic energy (and resulting velocity), rotational kinetic energy in the spinning wheels, and heat from friction. The fastest car is the one that starts with the most gravitational potential energy (weight in the back), ends up with the least rotational kinetic energy (light wheels with one lifted) and loses the least energy through friction (proper lubrication and alignment). Pinewood derby cars are a five ounce laboratory of practical physics, chemistry and engineering.

Potential and kinetic energy

We'll start out with the simplest possible case and then add more complexity to get more accuracy. First we consider a 141.7 gram (5 ounce) frictionless block sliding down an 8.53 m (28 foot) track where the car starts 1.219 m (4 feet) above the finish line. The energy that makes a pinewood derby car roll down the ramp is potential energy (symbol $U_g$). At the bottom of the ramp, this energy is converted into kinetic energy (symbol $E_k$).

The potential energy can be calculated using the formula

$U_g=mgh$.

where m is the mass of the car, $g$ is the acceleration due to gravity (9.807 m/s² = 32.17 ft/s² at the earth's surface) and h is the height of the car on the starting ramp (about 4 feet = 1.22 meters). The potential energy stored in a 5 ounce pinewood derby car is about 1.7 kg m²/s²= 1.7 J. The quantity 1.7 joule of energy is the same as 1.7 watts of power applied for one second.

The kinetic energy can be calculated using the formula

$E_k=\frac{1}{2}m{v}^2$.

where v is the velocity (speed) of the car, measured in meters per second (in SI units). If all of the potential energy is converted into kinetic energy, then

$U_g=E_k$

and, substituting from above,

$mgh=\frac{1}{2}m{v}^2$

since the mass is on both sides of the equation, you can divide both sides by $m$ and cancel (remove) the mass from the equation.

$gh=\frac{1}{2}{v}^2$

and, rearranging, the velocity is found from

$v=\sqrt{2gh}$

The velocity doesn't depend on the mass, just as Galileo demonstrated at the Leaning Tower of Pisa and, during the Apollo_15 landing, David Scott demonstrated on the moon. The velocity of any object falling from a height of 1.219 m is 4.890 m/s (11 MPH).

File:Apollo 15 feather and hammer drop.ogv

How fast does the block travel down the track? The fastest trip to the ground is straight down and the time to fall is the distance divided by the average speed, which is half of the final speed:

$t=\frac{d}{v/2}$.

The car takes 0.499 s to fall straight to the ground.

Now consider an 8.53 m (28 foot) track that consists of a 30° ramp followed by a flat portion to the finish. The ramp section is 2.43 m (8 feet) long and the flat section is 6.1 m (20 feet) long. The car travels the 2.43 m ramp at an average velocity of $v/2=$ 2.445 m/s and then travels the remaining 6.1 m at 4.890 m/s. The total time is

$t_{total}=t_{ramp}+t_{flat}$.

The block takes 0.992 s to go down the ramp and 1.245 s on the flat for a total of 2.237 s. The mass doesn't affect the speed - a frictionless feather is as fast as a lead brick.

Rotational kinetic energy

The rotational kinetic energy of the wheels is given by

$E_r=\frac{1}{2}I{\omega }^2$.

where I is the moment of inertia and ω is the angular velocity. The angular velocity is related to the linear velocity through

$\omega =rv$

Where $r$ is the radius of the wheel. The moment of inertia for a ring of radius r and mass $m^{\prime }$ is

$I_{ring}=m^{\prime }{r}^2$

and for a disk, it is

$I_{disk}=\frac{1}{2}{m}^{\prime }{r}^2$

For a Pinewood Derby wheel, the moment of inertia can be approximated by

$I_{wheel}=0.58m^{\prime }{r}^2$.

The rotational kinetic energy for the four wheel is therefore

$E_r=4\times 0.58m^{\prime }{\omega }^2{r}^2=\frac{1}{2}(2.32m^{\prime })v{}^2$.

This turns out to be 0.094 J of energy stored in the four wheels at the car's top speed of 4.75 m/s (see the table below). Compare that to the 1.7 J gravitational potential energy from above. Almost 6 % of that energy is stored in the spinning wheels and about 94 % is available for the car's forward velocity.

The potential energy relation is now

$U_g=E_k+E_r$,

$mgh=\frac{1}{2}(m{v}^2+2.32m^{\prime }v{}^2)$

and solving for the velocity

$v=\sqrt{\frac{2gh}{1+2.32\frac{m^{\prime }}{m}}}$

for a car of mass m with wheels of mass $m^{\prime }$. Now it is clear why the heaviest possible car is the fastest: for large m, the denominator approaches 1 and the velocity is the same as the above case for the frictionless block: 4.9 m/s. With standard 3.6 g wheels, a 141.7 g (5 ounce) car has a velocity of 4.75 m/s at the bottom of the track. A 113.4 g (4 ounce) car has a velocity of 4.72 m/s.

The advantage of light wheels is also clear. The slowest car is one with the most mass in the wheels. If $m^{\prime }=m$ (four 35 g wheels rolling down the track!) the velocity is 2.7 m/s. With 3.6 g wheels, the velocity is 4.75 m/s; with 1 g light wheels, the velocity is 4.85 m/s. Another way to look at it is that a light wheel car has less than 2 % of its kinetic energy in the wheels while the standard wheel car has almost 6 %.

Raising one wheel reduces the rotational energy as long as that wheel doesn't touch the ground. The velocity of a three wheel (3.6 g) car is 4.78 m/s, while a raised light wheel car can reach 4.86 m/s.

An idealized track

Now that we know how fast an idealized car can go, let's let it run down an idealized track. A typical pinewood derby track is 32 feet long with 4 feet for the starting gate and arresting gear, leaving 8.534 m for travel. The first part of the track has a slope of about 20°, a curved transition section, followed by a flat section to the finish. The track can be approximated by a straight ramp section with length $d_1$ followed by a flat section with length $d_2$. Times calculated using the straight track approximation differ by less than 0.001 s compared to those obtained using a curved track and numerical integration. With the straight track and 20° slope, $d_1$ = 3.564 m and $d_2$ = 4.970 m. The car travels down the sloped section $d_1$ starting at zero velocity and accelerating to a velocity $v$ with an average speed of $v/2$. It then travels the distance $d_2$ at a velocity $v$. The total time is then

$t=2\frac{d_1}{v}+\frac{d_2}{v}$

or 12.098/v seconds, if the velocity is specified in meters per second. Run times under different conditions are given in the table below.

Car Speeds and Times

Conditions	$h(m)$	$m(g)$	$m^{\prime }(g)$	$v(m/s)$	$t(s)$
Frictionless Block	1.219	any	0	4.89	2.47
Stock Wheels	1.219	141.7	3.6	4.75	2.55
Light (4 oz) Car	1.219	93.1	3.6	4.72	2.56
Light Wheels	1.219	141.7	1.0	4.85	2.49
One Raised Wheel	1.219	141.7	3.6	4.78	2.53
Light Wheels, One Raised	1.219	141.7	1.0	4.86	2.49
Rear Bias (Stock Wheels)	1.243	141.7	3.6	4.80	2.52

Center of Mass

Up to this point, we have approximated the car as a point mass that starts 1.219 m above the finish and winds up at 0 m. As anyone familiar with pinewood derby knows, it is usually best to keep the the center of mass as far back as possible, in part to increase the gravitational potential energy. How much faster is a car with the center of mass shifted to the back? Consider two cars, Car A with the center of mass at the center of the block and Car B with the center of mass 25.4 mm (one inch) in front of the rear axle in an extended wheelbase configuration with the axle 15.9 mm (5/8") from the rear of the block. The center of mass of the Car B is 47.6 mm behind Car A and 23.8 mm higher on a 30° slope. Car A starts at 1.219 m and (as shown above) has a maximum velocity of 4.75 m/s and 2.55 s time; Car B starts at 1.243 m and has a maximum velocity of 4.80 m/s and a 2.52 s time.

Friction

diagram showing the forces acting on a block that is resting on an inclined plane.

Friction is the force that opposes the motion of two objects in contact. There are four types of friction that slow a pinewood derby car:

1. Rolling resistance
2. Wheel-to-axle friction
3. Wind resistance
4. Contact friction

The last entry, contact friction, includes contact between the wheel inner hub and car body, the outer hub and the axle head, and between the wheel and the track guide rail. It is difficult to quantify contact friction because it depends on the wheel alignment, track surface and other factors that vary widely from race-to-race. Wheel to body and wheel to guide rail friction is reduced by coning and polishing the hub, shaving and polishing the inner rim and, overall, by assuring proper alignment.

Rolling resistance

There are two kinds of friction: static and kinetic. Static friction is the resistance of an object at rest, for example, a heavy box at rest on concrete floor. rolling resistance is the friction between a rolling wheel and surface. It is a static friction because, even though the wheel is moving, it is not sliding against the surface. Kinteic friction is the force that opposes the motion of a moving object. Using the box example, this would be the force that must be overcome as you slide the box across the floor. In the wheel example, rolling resistance is static, while skidding or doing a burnout involves kinetic friction. In this sense, rolling resistance is for the most part a "good" friction for a pinewood derby car because it does very little work and because it helps to convert what would otherwise be skidding friction into the significantly lower friction between the wheel and axle.

The force that results from rolling resistance is given by:

$F_{rr}=C_{rr}{N}_f$

where C_rr is the coefficient of rolling friction (CRF), and $N_f$ is the the normal force (perpendicular to the track). The CRF value for a low rolling resistance tire is about 0.002 (see the rolling resistance article). On a flat section of the track the normal force is perpendicular to the track and

$N_f=mg=0.1417kg\times 9.807m/s^2=1.390N$

therefore

$F_{rr}=0.002\times 1.390N=0.0028N$.

Car modifications that can reduce the CRF can reduce the rolling resistance by the same factor. For example, a "V" or "H" tread pattern limits the contact area between the wheel and track and thereby reduce the CRF and rolling resistance. Note that a raised wheel does not reduce the overall rolling resistance since the full weight of the car is distributed over the remaining three wheels and increases their rolling resistance. However, the rolling resistance is greater for the rear wheels in a rear biased car since they bear a greater fraction of the weight.

Wheel-to-axle friction

Tractor pulling contests involve high values of both static and kinetic friction

The equation for calculating friction is

$F_f=\mu N_f$,

where $F_f$ is the frictional force, $N_f$ is the normal force (perpendicular to the track) exerted between the surfaces, and $\mu$ is the coefficient of friction, which is a property of a particular system. The value of $\mu$ is about 0.24 for smooth plastic on metal and can be reduced to 0.1 if the axle is polished and graphite or other lubricant is used. The normal force is the force of the body mass on the axles

$N_f=(m-m^{\prime })g$,

Where $m-m^{\prime }$ is 127.3 g for a car at maximum weight with 3.6 g wheels. The wheel-to-axle friction is reduced by the mechanical advantage, which is the ratio of the wheel diameter to the axle hole diameter. For every rotation of the wheel, the car travels π times the 30.2 mm wheel diameter: 95.0 mm. The 2.29 mm axle bore travels only 7.19 mm around the axle per rotation. The wheel-to-axle friction is then

$F_f=\mu (m-m^{\prime })g\left(\frac{r}{r_A}\right)$,

where $r_A$ is the radius of the axle. Using the above values, the wheel-to-axle frictional force is 0.00946 N.

Note that the wheel-to-axle friction for a light wheel car is 8% larger than for the stock wheel car due to the greater mass of the body (137.7 g body plus four 1.0 g wheels). However, the frictional force can be cut in half using needle axles, which are allowed in some open class races. A 1 mm needle axle has a mechanical advantage of 30 and a frictional force of 0.00453 N (assuming light wheels).

The wheel-to-axle friction and rolling resistance are of comparable magnitude. From the above section, the rolling resistance was estimated to be about 0.003 N compared to the wheel-to-axle friction estimated above to be about three times larger.

Another result is that a raised wheel does nothing to reduce wheel-to-axle friction. A three wheel car simply distributes the weight among three axles rather than four and the frictional force is the same. All of the raised wheel advantage stems from rotational kinetic energy.

Wind resistance

Space shuttle showing the thermal tiles necessary to protect the craft from heating caused by wind resistance in the atmosphere.

Kinetic friction between a gas or liquid is called drag and the drag force on the car due to air friction can be calculated from

${𝐅}_d=\frac{1}{2}\rho v^{2}A{C}_d$

where F_d is the drag force ρ is the air density (about 1.2 kg/m³) v is the velocity, A is the frontal area of the car (0.0014 m² for an uncut block), C_d is the drag coefficient (about 0.4 for a typical car). Using the 4.75 m/s for a 5 ounce car with standard wheels gives a drag force of 0.0081 N. Using $F=ma$, we get an acceleration of -0.057 kgm/$s^2$, about 0.6% of the gravitational force, but still enough to slow the car from 4.75 m/s to 4.69 m/s on the flat section of the track alone. A numerical integration with a similar track resulted in an a run that was 1.8% slower. In practice, all cars experience some air drag, but a low and sleek design may have an advantage of a few hundredths of a second against a less aerodynamic car.

Measuring friction

The static and dynamic friction can be measured using the apparatus in Figure 1. From Newton's Second Law of Motion we know that the forces balance, therefore the normal force balances the gravitational force on the car

Figure 1. Measuring the coefficient of friction on a flat surface.

$N_f=mg$.

At the point where the mass M just balances the the static frictional force

$\mu N_f=mg$

and

$\mu =M/m$ .

Figure 2. Measuring the coefficient of friction on an inclined surface.

The reader can verify that, in the inclined case of Figure 2, the coefficient of friction is given by

$\mu =\frac{(\frac{M}{m}-\sin (\theta ))}{\cos (\theta )}$.

The kinetic friction can be determined using either of the above apparatus, but the procedure takes a bit more patience. Add or subtract from the mass M until the car moves at a constant velocity when pushed. At this point, the gravitational force is equal to the kinetic frictional force. The trick is that the car can neither accelerate nor decelerate; we want F=ma=0, but this time when the car is in motion.

Tribology

The molecular structure of graphite. The carbon atoms are the gray balls that form a hexagonal plane structure. The planes can easily slide across each other which makes bulk graphite slippery.

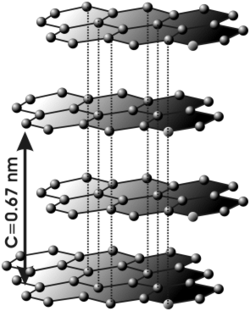
Tribology is the study of friction, lubrication and wear. Since friction is the force that slows a Pinewood Derby car and lubrication reduces friction, tribology is an essential science of the sport. Wear is not an important consideration since, as we have seen above, the forces are low. The lubricant must reduce the friction between the wheel and axle and also be compatible with the polystyrene wheels. Expanded polystyrene is known as styrofoam and makes a great cup for hot cocoa, but is a poor container for an orgainc solvent such as gasoline or naptha (ask your Dad about the old auto shop trick). Pure polystyrene can be crosslinked to form a copolymer with polybutadiene that is called high-impact polystyrene (HIPS) or high-impact plastic. HIPS is excellent for injection molding, so it is no coincidence that it is the material used for Pinewood Derby car wheels. Nonetheless, care must be taken to keep inappropraite solvents from lubricants, paints, or cleaners away from the wheels. Another consideration for lubrication is the possibility of fouling the track with excess lubricant, especially liquids. Some race rules permit only dry powder lubricants for this reason.

X-ray crystal structure of molybdenum disulfide, MoS₂. Molybdenum is blue and sulfur is yellow.

Graphite

Graphite, like diamond is one of the several forms of carbon. Unlike diamond, graphite is a poor gemstone, but it is an excellent lubricant. This is because the chemical bonds in diamond form a three dimensional structure, while the bonds in graphite form a two dimensional structure. The two dimensional sheets of graphite slide easily over each other, giving graphite powder its lubricating properties.

Molybdenum Disulfide

Molybdenum disulfide has the chemical formula MoS₂ and is similar in chemical structure to graphite in that it forms two-dimensional layers that slide upon each other. In pinewood derby applications, molybdenum disulfide powder is typically mixed with graphite powder.

Teflon

Teflon is the DuPont brand name for polytetrafluoroethylene (PTFE), which is a synthetic fluoropolymer (a fluorine containing polymer). Teflon has the lowest coeffieient of friction of any known solid material. It is used in powdered form as a Pinweood Derby lubricant.