Intermediate Algebra/Functions

See also: Calculus/Functions, Discrete mathematics/Functions and relations

---

Function as Box

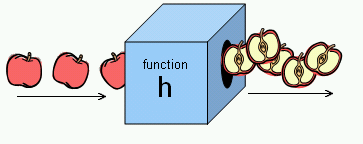
Functions are another way of describing certain things mathematically. They are often described as a machine in a box open on two ends; you put something in one end, something happens to it in the middle, and something pops out the other end. The function is the machine inside, and it's defined by what it does to whatever you give it.

Let's say the machine has a blade that slices whatever you put into it in two and sends one half out the other end. If you put in a banana, you'd get back half a banana. If you put in an apple, you'd get back half an apple.

Since this is algebra, the things that go in and come out of functions will be numbers. Let's define the function to take what you give it and cut it in half, that is, divide it by two. If you put in 2, you'd get back 1. If you put in 57, you'd get back 28.5. Functions are typically named with a single letter. We'll call this one h for half. (There's nothing special about the letter we choose--we could just as well called this function f. The letter doesn't have to stand for anything.)

Now we need the notation. To put 2 into the function, we write $h(2)$ (read h of 2). We know that

$h(2)=1$, and $h(57)=28.5$

but to completely explain this function, we can write this:

$h(x)=\frac{x}{2}$

What this means is that for any value of $x$, $h(x)$ equals $x$ divided by two. This form is called a function definition.

Some functions operate on multiple numbers. For instance,

$f(x,y,z)=x\cdot {\left(\frac{y}{2}\right)}^z$

Exercises

For exercises 1-6, algebraically define the function described.

Example: x) Three-quarters of a number
 Answer: $f(x)=3x/4$

1. Four-fifths of a number

2. A number added to itself five times

3. A number increased by three times the number

4. A number multiplied by itself seven times, then reduced by the number

5. One number reduced by a different number three times

6. Half a number times three more than another number

For exercises 7-9, evaluate.

Example: x) $f(x)=3x-4$
 a) $f(0)$ b) $f(4)$
 c) $f(1/3)$   d) $f(1/2)$
 
 Answer: a) $f(0)=3(0)-4=-4$     b) $f(4)=3(4)-4=8$
 c) $f(1/3)=3(1/3)-4=-3$ d) $f(1/2)=3(1/2)-4=-5/2$

7. $f(x)=10x$

a) $f(1)$
b) $f(1/2)$

c) $f(3.5)$
d) $f(-1)$

8. $g(x)=3x-1$

a) $g(4)$
b) $g(2/3)$

c) $g(1.1)$
d) $g(-3)$

9. $h(x)=x^2$

a) $h(7)$
b) $h(3/5)$

c) $h(5.3)$
d) $h(-6)$

Answers

Function as Relation

Functions can also be thought of as a subset of relations. A relation is a connection between numbers in one set and numbers in another.

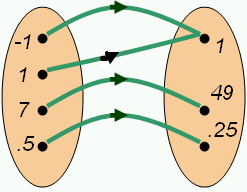
In other words, each number you put in is associated with each number you get out. The difference is that in a function, every 'input' number is associated with exactly one 'output' number whereas in a relation an 'input' number may be associated with multiple or no 'output' numbers. This is an important fact about functions. Notice that the relation depicted by the diagram above is not a function because it does not meet this requirement, unlike the relation depicted by the second diagram below, which is a function.

All functions are relations. Not all relations are functions.

Domain and Range

Domain

The domain of a function is the set of 'input' numbers for which the function is defined. The domain is part of the definition of a function. In the function in the illustration above, the domain is {-1,1,7,1/2}.

The natural domain of an algebraically-defined function is the set of numbers for which the function is defined.

In most algebra formulas, x is usually the variable associated with Domain.

Example

The function $f(x)=\sqrt{x}$ has a domain of $x\ge 0$ because the square root function is only defined for positive numbers (assuming that we are dealing with only real numbers).

Range

The range of a function is the set of results or solutions to the equation for a given input. A true function only has one result for every Domain.

In most algebra formulas, y is usually the variable associated with Range. As such, it can also be expressed f(x), which says that its value is a function of x.

Example

The function $f(x)=x^2$ has a range of $y\ge 0$ because the square of a number is always positive.

Functions in terms of Domain and Range

In taking both domain and range into account, a function is any mathematical formula that produces one result for each input. Hence, it can be said that in a valid function, Domain (x) and Range (y) have a many to one correspondance so that every given Domain value has one and only one Range value as a result, but not necessarily vice versa. This makes sense since results can repeat, but inputs cannot.

As a result, if x is horizontal and y is vertical, a function in terms of y (e.g. y = mx + b) will produce a set of results such that if intersected by a vertical line at any point on the graph it will only pass through the graph once. An asymptotic function (one with at least one undefined result) would also count as valid since it did not pass through more than one point of the graph. This is called the "vertical line" test.

It is important to note that the idea of domain and range can be applied to all relations and not just functions.

A Bit of Function Terminology

When speaking or writing about functions, different terminologies are used to describe how the functions work or what they do.

f of x Terminology

When we write $f(x)$, we say f of x. Thus, if we have a function defined with the equation $g(x)=\frac{x+2}{7}$ then we say that g of x equals the sum of x and 2 altogether divided by 7. This way, $g(5)=\frac{5+2}{7}=\frac{7}{7}=1$ so we would say that g of 5 equals 1.

The Value Of The Function At Terminology

If we have a function defined with the equation $g(x)=\frac{x+2}{7}$ then we say that The value of g at x is the sum of x and 2 altogether divided by 7. This way, $g(5)=\frac{5+2}{7}=\frac{7}{7}=1$

Piecewise-defined function

A function whose definition depends on the input.

Absolute value function

f(x)=|x|
or
$f(x)=\{\begin{array}{cc}x& \text{if }x\ge 0\\ -x& \text{if }x<0\end{array}$

One can interpret $|x|$ as the undirected distance between x and 0, (which is always non-negative). Going on, $|x-y|$ can be interpreted as the distance between the numbers x and y on the number line.

Even and odd functions

Even functions

An even function is defined as a function $f$ such that $f(-x)=f(x)$.
Geometrically an even function can be defined as a function that exhibits a mirror image symmetry across the y-axis (the vertical line that passes through the origin).

An example of an even function is $h(x)=x^2$ because $f(5)=25=f(-5)$ and because $f(x)=x^2=f(-x)$ for all real numbers x.

Odd functions

An odd function is defined as a function $f$ such that $f(-x)=-f(x)$.
Geometrically an odd function can be defined as a function that exhibits a 180 degree rotational symmetry about the origin.

An example of an odd function is $f(x)=x^3$ because for all real numbers x, $f(x)=x^3=-((-x{)}^3)=-f(-x)$ for example $f(2)=2^3=8=-((-2{)}^3)=-(-8)=-((-2{)}^3)=-f(-2)$

Composite function

A composite function $h$ can be defined as the composite of the two functions $f$ and $g$ and denoted as $h(x)=f(g(x))$ (read h of x is equal to f of g of x) or $h(x)=(f\circ g)(x)$.

Example:

Let $f(x)=2x+1$     $g(x)=5x-3$
 $h(x)=f(g(x))$
 $h(x)=f(5x-3)$
 $h(x)=2(5x-3)+1$
 $h(x)=10x-6+1$
∴$h(x)=10x-5$

Example:

Let $f(x)=-\sqrt{16-x}$     $g(x)=4x^2$
$(f\circ g)(x)=f(4x^2)$
$(f\circ g)(x)=-\sqrt{16-(4x^2)}$
$(f\circ g)(x)=-\sqrt{4(4-x^2)}$
$(f\circ g)(x)=-\sqrt{4}\sqrt{(4-x^2)}$
$(f\circ g)(x)=-2\sqrt{4-x^2}$
Domain: $-2\le x\le 2$
Range: $-4\le y\le 0$

Inverse function

The function $g$ is the inverse of the one-to-one function $f$ if and only if the following are true:

$g(f(x))=x$

$f(g(x))=x$

The inverse of function $f$ is denoted as $f^{-1}$ .

Geometrically $f^{-1}$ is the reflection of $f$ across the line $y=x$. Conceptually, using the box analogy, a function's inverse box undoes what the function's regular box does.

Example:

$f(x)=2x$
$f^{-1}(x)=\frac{1}{2}x$

$f(f^{-1}(x))=f(\frac{1}{2}x)$
$f(f^{-1}(x))=2(\frac{1}{2}x)$
$f(f^{-1}(x))=x$


$f^{-1}(f(x))=f^{-1}(2x)$
$f^{-1}(f(x))=\frac{1}{2}(2x)$
$f^{-1}(f(x))=x$

To find the inverse of a function, remember that when we use $f^{-1}(x)$ as an input to $f$ the result is $x$. So start by writing $x=f(f^{-1}(x))$ and solve for $f^{-1}$

Example:

Suppose:$f(x)=2x+1$
Then $x=f(f^{-1}(x))$
$x=2f^{-1}(x)+1$
$x-1=2f^{-1}(x)$
$f^{-1}(x)=\frac{x-1}{2}$

The Domain of an inverse function is exactly the same as the Range of the original function. If the Range of the original function is limited in some way, the inverse of a function will require a restricted domain.

Example:

$f(x)=\sqrt{x-1}$         
$x=f(f^{-1}(x))$
$x=\sqrt{f^{-1}(x)-1}$         
$x^2={\sqrt{f^{-1}(x)-1}}^2$         
$x^2=f^{-1}(x)-1$            
$f^{-1}(x)=x^2+1$            
The Range of $f(x)$ is $f(x)\ge 0$. So the Domain of $f^{-1}(x)$ is $x\ge 0$.

One-to-one function

A function that for every input there exists an output unique to that input.

Equivalently, we may say that a function $f$ is called one-to-one if for all $x,x^{\prime }\in A,f(x)=f(x^{\prime })$ implies that $x=x^{\prime }$ where A is the domain set of f and both x and x' are members of that set.

Horizontal Line Test
If no horizontal line intersects the graph of a function in more than one place then the function is a one-to-one function.

Previous: Further Arithmetic in Introduction to algebra
Next: Function Graphing

Creating Functions

functions sometimes must be created in order to represent scalable quantities. The application of creating equations based on diagrams is essentially useful for graphing, and representing a certain model for the figure.

Equations

Creating equations from given data:

figuring out the slope of a line

if the line goes through the origin (0,0) and the point (1,2)

Given the equation, M = (y2 - y1) / (x2-x1)

1. First recognize what is x1,y1 and x2,y2

  Usually x2 and y2 are the data set to the right while x1 and y1 are the dataset to the left

   x1,y1    x2, y2
   0 , 0    2 , 1

2. Now simply "plug and chug"

      (1 - 0)  1
   M=  ----- = --
      (2 - 0)  2

Reconizing that the equation of a graph would be:

   Y = Mx + B

   where M = Slope
         B = y-intercept

  (ex) M = 5, Y intercept = 3

  Y = (5)x + (3)  

Data and discovering their patterns by writing down the equation Usually these are applied in word problems

Usually, it would have a general "referance" variable and generally you have to derive equations from their relationships. Such as

Jenny has sold X amount of candy bars Tom has sold 2 times the amount than jenny They both sold a total of 30 candy bars

If they were told to write an equation, than they should think of the following:

Total = Something must be equal to 30.
both = meaning them both, means they should be added together.

First, we'll say the equation is Jenny + Tom = 30
But, to figure out this problem, we want to know what the reference variable is.
Since Tom sold twice, meaning 2 times the amount of jenny, than we could change the
equation in terms of jenny

1(Jenny) + 2(Jenny) = 30 bars
  3(jenny)          = 30 bars
              Jenny = 10 bars

Shape

It can be geometrically concluded by looking at a square, that half a square is simply a triangle.

if the area of a box is A = Length x width, than half a box which is a triangle should than be 1/2 length x width

Next: Algebra/Function graphing

Go to: Algebra/Additional function and relation graphing

[[Category:Algebra|Template:FULLCHAPTERNAME]]