Algebra/Ellipse

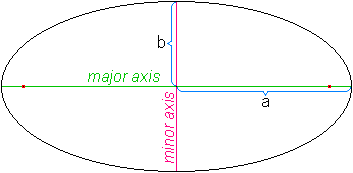
An ellipse is the collection of points that are equidistant from two points, called foci (singular focus).

The foci are found on the major axis, which has a length of 2a. The minor axis is 2b, and is smaller.

The "roundness" or "longness" of an ellipse can be measured by eccentricity. If c is the distance from the center to a focus, then e = c / a.

The latus rectum is a line parallel to the minor axis that crosses through a focus. Its length is b² / a.

"Long" ellipses are generally written as

$\frac{(x-h{)}^2}{a^2}+\frac{(y-k{)}^2}{b^2}=1$

where (h,k) is the center, while "tall" ellipses are written as

$\frac{(y-k{)}^2}{a^2}+\frac{(x-h{)}^2}{b^2}=1$