Astronomy/Kepler's Laws
Main Page - Astronomy - Positional astronomy
Johannes Kepler was a mathematician who attempted to derive a set of fundamental principles which would explain the motions of the planets. He believed in the heliocentric view of the solar system proposed by Copernicus, and he also possessed a rich set of observations of the planets made by Tycho Brahe.
After twenty years of painstaking attempts and various discarded ideas based on geometry, he finally arrived at a mathematical model of orbital motions based on the ellipse. Kepler summarized his findings in the form of three laws of planetary motion:
- The Law of Orbits — The orbits of the planets are ellipses, with the sun at one focus.
- Law of Areas — The line between a planet and the sun sweeps out equal areas in the plane of the planet's orbit over equal times.
- The Law of Periods — The time required for a planet to orbit the sun, called its period, is proportional to half the long axis of the ellipse raised to the 3/2 power. The constant of proportionality is the same for all the planets.
At that time he developed these laws, there was not yet a developed theory of gravity capable of explaining why the planets moved as they were observed to. Later, Isaac Newton, using his universal inverse-square law theory of gravity, was able to show how Kepler's Laws fit into a scientific theory of celestial mechanics.
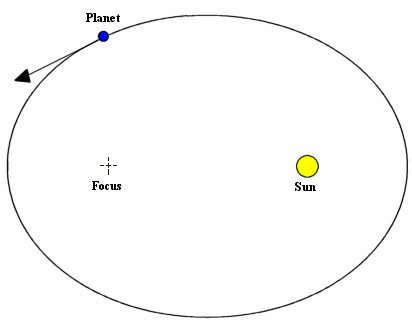
|
| Planet following an elliptical orbit with the Sun at a focus. |
Elliptical orbits
An ellipse is a shape formed by taking a diagonal slice through a cone. It is essentially the shape of a circle viewed at an angle.
An ellipse can be drawn by taking a piece of paper, two push-pins, a loop of string, and a pencil. The two pins are pushed through the paper into a suitable surface, providing the two foci for the ellipse. They should be closer together than the loop is long. The loop of string is placed around the base of these pins, leaving some slack. The pencil is now placed so that the pins and the loop form a triangle with a slight tension on the string.
Now try to draw a shape by moving the pencil about the pins while keeping the string taunt. The result should be an ellipse. The shape of the ellipse can be varied either by moving the pins closer together or further apart.
Kepler's second law says in brief that an object speeds up as it gets closer to the Sun and slows down as it moves further away. Where the distance from the Sun to the orbital path is longer, only a smaller arc needs to be traversed to sweep out an area that requires a wider arc near the Sun.
As the planet moves closer to the Sun along its orbit the gravitational force works to increase the velocity. In contrast, as the planet is moving further away, the gravity of the Sun gradually decelerates the body and it is slowed down.

|
| A planet in orbit about the Sun sweeps out equal areas A in the same time interval t. |
A line that divides an ellipse in half and passes through the widest part of the ellipse is called the major axis. A line perpendicular to this axis and dividing the ellipse in half is called the minor axis. Half the length of the major axis is called the semi-major axis, and is represented by a. The period required for a planet to complete one full orbit is represented by P. Mathematically then, by squaring both sides, Kepler's third law can be represented as follows:
where the alpha symbol (α) means "proportional to".
The ratio of the semi-major axis to the distance of a focus from the center of an ellipse is called the eccentricity of the orbit. When the two foci of the ellipse are on top of each other, the eccentricity is exactly 0.0 and the shape is a circle. As the eccentricity increases, the orbiting planet moves much further away than at the closest approach. The orbital eccentricity for planets in our Solar system varies from as much as 0.25 for Pluto down to 0.0068 for Venus.
The scientific name for the point of closest approach is the periapsis, while the most distance separation is the apoapsis. In the case of planets orbiting the Sun, these are called the perihelion and aphelion, respectively. (The -helion suffix comes from the Greek name for the Sun deity, Helios. This word is also the source of the name for the element Helium.)
The second and third laws provide a basis for calculating the period of any planet orbiting the Sun, as well as determining where the planet will be located along the orbital path.

|
| Two elliptical orbits with the same major axis a but different eccentricity. |
Perhaps the counter-intuitive aspect of the third law is that for any two identical bodies orbiting the Sun with the same semi-major axis, the orbital period is the same. This is true even if one is orbiting in a perfect circle and the other has an orbit that is highly elliptical (has a relatively high eccentricity). The elliptical shape will fit entirely within the circle except at two points, so it is actually a shorter orbital path. However the perihelion of the ellipse will be located further from the Sun, so the planet will spend more time traversing the distant section of the orbit. The shorter orbit and the slower traverse of the perihelion compensate for each other, resulting in an identical period with the circular orbit.