Optics/Refraction

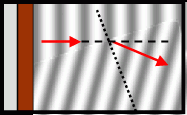
When light travells from one medium to another, it bends.

When light travels from one medium to another, it bends either towards or away the normal as a result of the change in its velocity. This is why objects that are submerged in water tend to appear fatter.

When going from a less optically dense to a more optically dense medium, light bends towards the normal and decreases in velocity. When going from a more optically dense to a less optically dense medium, light bends away from the normal and increases in velocity. It is important to note that optical density is different from normal density.

Snell's law tells us how much the light will refract: $n_1\sin {\theta }_1=n_2\sin {\theta }_2$

$n_1$ and $n_2$ are the indices of refraction, with the value $n=c/v$, the ratio of the speed of light in a vacuum to the speed of light in the medium in question.

Note that $n=1$ if the medium is air; the approximation is close enough to be generally useful.

The greater the value of $n$, the less the speed of light in that medium. If $n_1$ is less than $n_2$, it follows that $\sin {\theta }_1$ is greater than $\sin {\theta }_2$ (by Snell's law of refraction, above). Since $\theta$ can never be greater than 90 degrees, then if $\sin {\theta }_1>\sin {\theta }_2$ then ${\theta }_1>{\theta }_2$; that is, the angle of incidence is greater than the angle of refraction.

Here is a sample calculation showing how light bends when travelling from air (refractive index of about 1) to water (refractive index of about 1.33):

$n_1\sin {\theta }_1=n_2\sin {\theta }_2$

$1.00\sin 45=1.33\sin {\theta }_2$

$\frac{1.00\sin 45}{1.33}=\sin {\theta }_2$

${\theta }_2={\sin }^{-1}\frac{1.00\sin 45}{1.33}$

${\theta }_2=32.12$

To understand how the refraction of light works, you may download a free software from the following site.

• Refraction of rays software (Windows executable)