Astrodynamics/Fundamental Laws

Laws of Motion

All of the mathematics involved in astrodynamics are derived from the classical equations of motion, and so this is where we will begin our study. Even though Newton derived his three laws of motion nearly 50 years after Kepler first stated his own three laws of planetary motion, we will start our study with Newton.

Newton's Laws

First Law (Law of Inertia)

A body in motion tends to remain in motion in the same speed and direction unless acted upon by an external force. A body at rest tends to remain at rest unless acted upon by an external force.

Second Law (Law of Force)

The rate of change of the speed of an object, its acceleration, is proportional to the force applied on that object, and occurs in the same direction as that force.

Third Law

To every action there is always an equal but opposite reaction.

The second law is typically written by the equation F = ma, where a is the acceleration of the object, m is the mass of the object, and F is the amount of force applied. However, the second law also stipulates that the acceleration has a direction associated with it, and that direction is the same as the direction of the applied force. We must re-write this equation using vectors to account for the direction of the force and the acceleration. We can write this instead as F= ma, where F is the vector for force, and a is the vector for acceleration. We will not define specifically what items these vectors contain, because as we will see shortly, it is very much dependant on the problem.

In space, there is never a single force acting on an object, gravitational pulls from all objects in the universe play some role. However, because the force that gravity exerts on an object decreases with distance, objects that are very far away produce negligible force, and can typically be ignored. However, consider a situation of a satellite orbiting around the earth: that satellite is being affected by gravity from the earth, from the moon, and to a lesser extent from the sun. We can sum these forces together to produce a more general form of the second law:

$\sum F=m𝐚$

The third law also produces an interesting result, and one that is going to shape many calculations. In space travel there are two types of motion: powered and un-powered. In a powered device, such as a rocket, for the body to be "pushed" forward, it must push something backward with equal force. In the case of a rocket, burnt fuel is pushed out the back of the rocket, in order to move the body of the rocket forward. As a result of the third law, any powered space craft will have non-constant mass, which will introduce additional complexity into our calculations. If we have two bodies, 1 and 2, and they are pushing against each other, we can say that the force exerted by body 1 on body 2 is equal in magnitude, but opposite in direction, from the force exerted by body 2 on body 1. In other words, we can say:

$F_{12}=-F_{21}$

We will use these laws throughout the book.

Kepler's Laws

First Law

The orbit of a planet is an ellipse with the sun at one of the foci of that ellipse.

Second Law

The line joining the planet to the sun sweeps out equal areas in equal periods of time.

Third Law

The square of the planet's period is proportional to the cube of it's average distance from the sun.

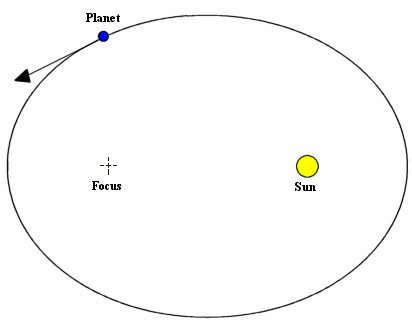
As we remember from algebra, an ellipse is a conic section formed from two foci, where the sum of the distances from the ellipse to each focus is equal. The sun is at one focus, and the other focus is an imaginary point in space.

This picture is an orbit in the form of an ellipse with the sun at one of the foci. We call the focus that contains the central body the prime focus, and the other focus, which has no physical significance as the secondary focus.

This picture is a demonstration of Kepler's second law:

As we can see, for the line joining the planet (dashed lines) to sweep out triangular sections of equal areas, it must move slower as the planet gets further from the sun. When the planet is closer to the sun, it must be traveling faster in order to sweep out equal areas in equal time.

For a similar example, consider a bouncing ball. The ball is moving slowest at the top of its arc, and continues to gain speed as it travels downward towards the earth. As the earth moves away from the sun, gravity decelerates the planet. When the planet is moving towards the sun, gravity is accelerating the planet.

Newton's Law of Universal Gravitation

Newton's law of gravity is another common law, and one that is of prime importance in the study of astrodynamics. Stated in it's most simple form, the law of gravity is: Template:- Template:Eqn

$F_g=-\frac{G{m}_1{m}_2}{r^2}$

We know that the law of gravity is directional, that is that the force of gravity works to pull two bodies together, along the straight line between them. The image below shows two bodies, M₁ and M₂ being attracted to each other through the force of gravity acting along the line between their centers of gravity:

The force acting on M₁ is denoted as F₁₂, and the force acting on M₂ is denoted as F₂₁. We know from Newton's third law of motion that the two forces must be equal in magnitude, but oposite in direction:

${𝐅}_{12}=-{𝐅}_{21}$

Because the direction of the force is important, we vectorize the law of universal gravitation equation as well:

${𝐅}_g=-\frac{G{m}_1{m}_2}{r^2}\frac{𝐫}{r}$

Where r is the distance vector between the two bodies, and r is the scalar distance between the two. F_g is the force vector of gravity.

Gravitational Constant

The big G' is called the gravitational constant. It is equal to:

$G=6.67428\times 10^{-11}{\text{m}}^3{\text{kg}}^{-1}{\text{s}}^{-2}$

Coordinate Systems

We are going to discuss coordinate systems again at some length, but we can introduce some of the basic concepts right now. A vector requires an origin and a coordinate system. The vector represents a magnitude and a direction, with the direction being from the origin to the end of the vector. Therefore, we need to settle on a coordinate system for our equations of gravity to make any sense.

Write out for both bodies:

${𝐅}_{12}=\frac{G{M}_1{M}_2}{r_{12}^3}{𝐫}_{12}$

${𝐅}_{21}=\frac{G{M}_1{M}_2}{r_{21}^3}{𝐫}_{21}$

These are the equations of motion for body 1 and body 2 in a generalized coordinate system. Note that Newton's Third Law gives: F₁₂ = - F₂₁ since r₁₂ = -r₂₁. Now we can create a new vector r:

$𝐫={𝐫}_{12}={𝐑}_2-{𝐑}_1$

System with an arbitrary coordinate system	System with origin at the center of M1

We can see from the equation above that if we have an arbitrary coordinate system, we can replace it with a coordinate system whose origin is the center of one of the bodies. This simplifies our equations significantly, because we only need to account for 1 position vector and 1 force vector instead of 2 for each.