Circuit Theory/RLC Circuits
Template:Circuit Theory/Page Template:Wikipedia
Series RLC Circuit
Circuit Impedance
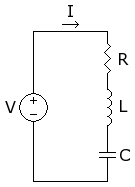
- Zt = ZR + ZL + ZC
- Zt = R + jωL + 1 / jωC
- Zt = jωRC + (jω)2LC + 1
- Zt = (jω)2LC + jωRC + 1
- Zt = (jω)2 + jω(R/L) + 1/LC
Frequency Response of the circuit
- There is one frequency at which ZC = ZL
- jωL = 1 / jωC
- The Frequency is called Resonance Frequency
- When there is no applied voltage, there will be no current. Therefore, the impedance of the circuit is zero.
- Zt = (jω)2 + jω(R / L) + (1 / LC) = 0
Take the derivative of both sides:
- 2jω + R / L = 0
- The Frequency is called Damping Factor. The Damping Factor of the series RLC is . In other words, the damping factor of the series RLC is equal to half of the Response Frequency of the inductor.
Compare the resonant frequency with the damping factor. We have three situations depending on the relationship between these values:
- The Resonant Frequency = the Damping Factor (). The circuit is Critical Damped
- The Resonant Frequency > the Damping Factor (). The circuit is Over Damped
- The Resonant Frequency < the Damping Factor (). The circuit is Under Damped
Parallel RLC Circuit
Circuit Impedance

- 1/Z = 1/ZR + 1/ZL + 1/ZC
- 1/Z = 1/R + 1/jωL + jωC
- 1/Z = jωL + R + (jω)2RLC / jωLR
- 1/Z = (jω)2RLC + jωL + R / jωLR
Frequency Response of the Circuit
- There is one frequency at which ZC = ZL
- jωL = 1 / jωC
- The Frequency is called The Resonant Frequency.
- When there is no applied voltage . There will be no current . Therefore, the circuit Impedance is zero
- Z = (jω)2 + jω(1/RC) x + (1/LC) = 0
- Take deravative of both sides
- 2jω + 1 / RC = 0
- ω =
- The Frequency ½ (1 / RC) is called the Damping Factor.
- The Damping Factor of the parallel RLC is ½ (1 / RC) . In other words, the damping factor of the parallel RLC is equal half of the Response Frequency of the capacitor.
Compare the resonance frequency with the damping factor, we have the following three situations:
- The Resonant Frequency = the Damping Factor . The circuit is Critical Damp
RLC series Critically Damped - 1 / γ(LC) = ½ (R / L)
- Z = (jω)2 + jω(1/RC) x + (1/LC) = 0 . This equation only has one root
- Because the resonance frequency is equal to the damping factor. Therefore, the square root is zero.
- For arbitrary constants A and B. Critically damped circuits typically have low overshoot, no oscillations, and quick settling time.
- The Resonant Frequency < the Damping Factor . The circuit is Under Damp
- γ(L / C) > ½ (R / L)
- Z = (jω)2 + jω(1/RC) x + (1/LC) = 0 . This equation has 2 imaginaries Roots
- Because The Resonance Frequency is greater than the Damping Factor . Therefore , The Square Roots is negative . And Square Root of a negative number is an imaginary number
- is a negative number, and square root of a negative number is an imaginary number.
- and
- Where:
- The solutions are:
- For arbitrary constants A and B. Using Euler's formula, we can simplify the solution as:
- For arbitrary constants C and D. These solutions are characterized by exponentially decaying sinusoidal response. The higher the Quality Factor (below), the longer it takes for the oscillations to decay.
- The Resonant Frequency > the Damping Factor . The circuit is Over Damp
RLC series Over-Damped Response - γ(L / C) < ½ (R / L)
- Z = (jω)2 + jω(1/RC) x + (1/LC) = 0 . This Equation has 2 Real Roots
- Because The Resonant Frequency is greater than the Damping Factor. Therefore , The Square Root is a positive number
- Overdamped circuits are characterized as having a very large settling time, and possibly a large steady-state error.
Resonance
A circuit containing resistors, capacitors, and inductors is said to be in resonance when the reactance of the inductor cancels that of the capacitor to leave the resulting total resistance of the circuit to be equal to the value of the component resistor. The resonance state is achieved by fine tuning the frequency of the circuit to a value where the resulting impedance of the capacitor cancels that of the inductor, resulting in a circuit that appears entirely resistive.
In other words, the resonant frequency of the circuit is the frequency where the circuit impedance is the lowest, and the circuit produces the highest output gain. We define the resonant frequency of an RLC circuit as:
Damping Factor
The damping factor is the amount by which the oscillations of a circuit gradually decrease over time. We define the damping ratio to be:
| Circuit Type | Series RLC | Parallel RLC |
|---|---|---|
| Damping Factor | ||
| Resonance Frequency |
Compare The Damping factor with The Resonance Frequency give rise to different types of circuits: Overdamped, Underdamped, and Critically Damped. We will discuss these terms in the next chapter.
Bandwidth
For series RLC circuit:
For Parallel RLC circuit:
Quality Factor
For Series RLC circuit:
For Parallel RLC circuit:
Stability
Because inductors and capacitors act differently to different inputs, there is some potential for the circuit response to approach infinity when subjected to certain types and amplitudes of inputs. When the output of a circuit approaches infinity, the circuit is said to be unstable. Unstable circuits can actually be dangerous, as unstable elements overheat, and potentially rupture.
A circuit is considered to be stable when a "well-behaved" input produces a "well-behaved" output response. We use the term "Well-Behaved" differently for each application, but generally, we mean "Well-Behaved" to mean a finite and controllable quantity.
Second-Order Solution
The solution proceedures for the second-order circuit is a sufficiently complex-enough task that we are going to devote the entire next page to it. See: Second-Order Solution.
Conclusion
| Cicuit | Ký Hiệu | Series RLC | Parallel RLC |
|---|---|---|---|
| Cicuit |  |
 | |
| Impedance | Z | ||
| Roots | λ | λ = | λ = |
| I(t) | Aeλ1t + Beλ2t | Aeλ1t + Beλ2t | Aeλ1t + Beλ2t |
| Damping Factor | |||
| Resonant Frequency | |||
| Band Width | |||
| Quality factor |