A-level Mathematics/M1/Linear Momentum

Objectives

By the end of this chapter you should be able to do the following:

Use (and recall) the definition of linear momentum, and show an understanding of it's vector nature in 1 dimension.

Understand and use conservation of linear momentum, in 1 dimension, and solve simple problems involving direct collision of two bodies before and after impact.

Momentum as a vector

Because momentum is defined to be mass times velocity, momentum is the product of a scalar and a vector, which is ultimately a vector.

$p=mv$

Conservation of Momentum

Within a closed system (Ie a system not subject to an external influence) momentum is always conserved. Due to this, we can easily derive the following formula that is used in working out momentum:

$(M_1*U_1)+(M_2*U_2)=(M_1*V_1)+(M_2*V_2)$

Where:

M = Mass U = Initial Velocity V = Velocity after collison

Whatever the momentum on the LHS, the total momentum on the RHS will be the same.

Collisions

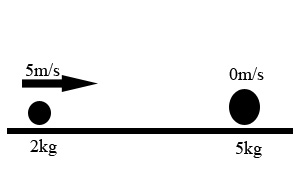
The conservation of momentum is best illustrated through an example question:

The system before the collision.

The system after the collision.

As we have all the values before the collision, we can use the formula above to work out the total momentum in the system:

$(2*5)+(5*0)=10Ns$

Now we know that momentum before = momentum after. So, 10 = (2 * 10) + (5 * ?). This may seem to be unworkable at first, but because velocity is a vector and the two balls are rolling in opposite directions, the 5kg ball has a negative velocity.

Rearranging our formula we get 10 - 20 = 5 * ?. Rearranging this again to $(10-20)/5=?$ we can see that $?=-2m{s}^{-}1$