Calculus/Further integration techniques

We have already considered two major techniques we can use to solve integration problems, that of the method of substitution, and integration by parts.

Here we make use of these techniques to help us integrate complicated integrals.

Partial fractions

First, an example. Suppose we want to find $\int \frac{3x+1}{x^2+x}dx$. One way to do this is to simplify the integrand by finding constants $A$ and $B$ so that

$\frac{3x+1}{x^2+x}=\frac{3x+1}{x(x+1)}=\frac{A}{x}+\frac{B}{x+1}.$

This can be done by cross multiplying the fraction which gives $\frac{3x+1}{x(x+1)}=\frac{A(x+1)+Bx}{x(x+1)}.$ As both sides have the same denominator we must have $3x+1=A(x+1)+Bx$. This is an equation for $x$ so must hold whatever value $x$ is. If we put in $x=0$ we get $1=A$ and putting $x=-1$ gives $-2=-B$ so $B=2$. So we see that

$\frac{3x+1}{x^2+x}=\frac{1}{x}+\frac{2}{x+1}$

Returning to the original integral

$\int \frac{3x+1}{x^2+x}dx$	=	$\int \frac{dx}{x}+\int \frac{2}{x+1}dx$
	=	$\ln \left|x\right|+2\ln |x+1|+C$

Rewriting the integrand as a sum of simpler fractions has allowed us to reduce the initial integral to a sum of simpler integrals. In fact this method works to integrate any rational function.

Method of Partial Fractions:

• Step 1 Use long division to ensure that the degree of $P(x)$ less than the degree of $Q(x)$.
• Step 2 Factor Q(x) as far as possible.
• Step 3 Write down the correct form for the partial fraction decomposition (see below) and cross multiply to find the constants.

To factor Q(x) we have to write it as a product of linear factors (of the form $ax+b$) and irreducible quadratic factors (of the form $a{x}^2+bx+c$ with $b^2-4ac<0$).

Some of the factors could be repeated. For instance if $Q(x)=x^3-6x^2+9x$ we factor $Q(x)$ as

$Q(x)=x(x^2-6x+9)=x(x-3)(x-3)=x(x-3{)}^2.$

It is important that in each quadratic factor we have $b^2-4ac<0$, otherwise it is possible to factor that quadratic piece further. For example if $Q(x)=x^3-3x^2-2x$ then we can write

$Q(x)=x(x^2-3x+2)=x(x-1)(x+2)$

We will now show how to write $P(x)/Q(x)$ as a sum of terms of the form

$\frac{A}{(ax+b{)}^k}$ and $\frac{Ax+B}{(a{x}^2+bx+c{)}^k}.$

Exactly how to do this depends on the factorization of $Q(x)$ and we now give four cases that can occur.

Case (a) Q(x) is a product of linear factors with no repeats.

This means that $Q(x)=(a_{1}x+b_1)(a_{2}x+b_2)...(a_{n}x+b_n)$ where no factor is repeated and no factor is a multiple of another.

For each linear term we write down something of the form $\frac{A}{(ax+b)}$, so in total we write

$\frac{P(x)}{Q(x)}=\frac{A_1}{(a_{1}x+b_1)}+\frac{A_2}{(a_{2}x+b_2)}+\cdots +\frac{A_n}{(a_{n}x+b_n)}$

Example 1

Find $\int \frac{1+x^2}{(x+3)(x+5)(x+7)}dx$

Here we have $P(x)=1+x^2,Q(x)=(x+3)(x+5)(x+7)$ and Q(x) is a product of linear factors. So we write

$\frac{1+x^2}{(x+3)(x+5)(x+7)}=\frac{A}{x+3}+\frac{B}{x+5}+\frac{C}{x+7}$

Multiply both sides by the denominator

$1+x^2=A(x+5)(x+7)+B(x+3)(x+7)+C(x+3)(x+5)$

Substitute in three values of x to get three equations for the unknown constants,

$\begin{array}{cc}x=-3& 1+3^2=2\cdot 4A\\ x=-5& 1+5^2=-2\cdot 2B\\ x=-7& 1+7^2=(-4)\cdot (-2)C\end{array}$

so $A=5/4,B=-13/2,C=25/4$, and

$\frac{1+x^2}{(x+3)(x+5)(x+7)}=\frac{5}{4x+12}-\frac{13}{2x+10}+\frac{25}{4x+28}$

We can now integrate the left hand side.

$\int \frac{1+x^{2}dx}{(x+3)(x+5)(x+7)}=\frac{5}{4}\ln |x+3|-\frac{13}{2}\ln |x+5|+\frac{25}{4}\ln |x+7|+C$

Case (b) Q(x) is a product of linear factors some of which are repeated.

If $(ax+b)$ appears in the factorisation of $Q(x)$ k-times. Then instead of writing the piece $\frac{A}{(ax+b)}$ we use the more complicated expression

$\frac{A_1}{ax+b}+\frac{A_2}{(ax+b{)}^2}+\frac{A_3}{(ax+b{)}^3}+\cdots +\frac{A_k}{(ax+b{)}^k}$

Example 2

Find $\int \frac{1}{(x+1)(x+2{)}^2}dx$

Here P(x)=1" and "Q(x)=(x+1)(x+2)² We write

$\frac{1}{(x+1)(x+2{)}^2}=\frac{A}{x+1}+\frac{B}{x+2}+\frac{C}{(x+2{)}^2}$

Multiply both sides by the denominator $1=A(x+2{)}^2+B(x+1)(x+2)+C(x+1)$

Substitute in three values of x to get 3 equations for the unknown constants,

$\begin{array}{cc}x=0& 1=2^{2}A+2B+C\\ x=-1& 1=A\\ x=-2& 1=-C\end{array}$

so A=1, B=-1, C=-1, and

$\frac{1}{(x+1)(x+2{)}^2}=\frac{1}{x+1}-\frac{1}{x+2}-\frac{1}{(x+2{)}^2}$

We can now integrate the left hand side. $\int \frac{1}{(x+1)(x+2{)}^2}dx=\ln \frac{x+1}{x+2}+\frac{1}{x+2}+C$

Case (c) Q(x) contains some quadratic pieces which are not repeated.

If $(a{x}^2+bx+c)$ appears we use $\frac{Ax+B}{(a{x}^2+bx+c)}.$

Case (d) Q(x) contains some repeated quadratic factors.

If $(a{x}^2+bx+c)$ appears k-times then use

$\frac{A_{1}x+B_1}{(a{x}^2+bx+c)}+\frac{A_{2}x+B_2}{(a{x}^2+bx+c{)}^2}+\frac{A_{3}x+B_3}{(a{x}^2+bx+c{)}^3}+\cdots +\frac{A_{k}x+B_k}{(a{x}^2+bx+c{)}^k}$

Trigonometric Substitution

If the integrand contains a single factor of one of the forms $\sqrt{a^2-x^2}\text{ or }\sqrt{a^2+x^2}\text{ or }\sqrt{x^2-a^2}$ we can try a trigonometric substitution.

• If the integrand contains $\sqrt{a^2-x^2}$ let $x=a\sin \theta$ and use the identity $1-{\sin }^2\theta ={\cos }^2\theta .$
• If the integrand contains $\sqrt{a^2+x^2}$ let $x=a\tan \theta$ and use the identity $1+{\tan }^2\theta ={\sec }^2\theta .$
• If the integrand contains $\sqrt{x^2-a^2}$ let $x=a\sec \theta$ and use the identity ${\sec }^2\theta -1={\tan }^2\theta .$

Sine substitution

This substitution is easily derived from a triangle, using the Pythagorean Theorem.

If the integrand contains a piece of the form $\sqrt{a^2-x^2}$ we use the substitution

$x=a\sin \theta dx=a\cos \theta d\theta$

This will transform the integrand to a trigonometic function. If the new integrand can't be integrated on sight then the tan-half-angle substitution described below will generally transform it into a more tractable algebraic integrand.

Eg, if the integrand is √(1-x²),

$\begin{array}{ccc}\underset{0}{\overset{1}{\int }}\sqrt{1-x^2}dx& =& \underset{0}{\overset{\pi /2}{\int }}\sqrt{1-{\sin }^2\theta }\cos \theta d\theta \\ & =& \underset{0}{\overset{\pi /2}{\int }}{\cos }^2\theta d\theta \\ & =& \frac{1}{2}\underset{0}{\overset{\pi /2}{\int }}1+\cos 2\theta d\theta \\ & =& \frac{\pi }{4}\end{array}$

If the integrand is √(1+x)/√(1-x), we can rewrite it as

$\sqrt{\frac{1+x}{1-x}}=\sqrt{\frac{1+x}{1+x}\frac{1+x}{1-x}}=\frac{1+x}{\sqrt{1-x^2}}$

Then we can make the substitution

$\begin{array}{cccc}\underset{0}{\overset{a}{\int }}\frac{1+x}{\sqrt{1-x^2}}dx& =& \underset{0}{\overset{\alpha }{\int }}\frac{1+\sin \theta }{\cos \theta }\cos \theta d\theta & 0<a<1\\ & =& \underset{0}{\overset{\alpha }{\int }}1+\sin \theta d\theta & \alpha ={\sin }^{-1}a\\ & =& \alpha +{[-\cos \theta ]}_0^{\alpha }& \\ & =& \alpha +1-\cos \alpha & \\ & =& 1+{\sin }^{-1}a-\sqrt{1-a^2}& \end{array}$

Tangent substitution

This substitution is easily derived from a triangle, using the Pythagorean Theorem.

When the integrand contains a piece of the form $\sqrt{a^2+x^2}$ we use the substitution

$x=a\tan \theta \sqrt{x^2+a^2}=a\sec \theta dx=a{\sec }^2\theta d\theta$

E.g, if the integrand is (x²+a²)^-3/2 then on making this substitution we find

$\begin{array}{cccc}\underset{0}{\overset{z}{\int }}{(x^2+a^2)}^{-\frac{3}{2}}dx& =& a^{-2}\underset{0}{\overset{\alpha }{\int }}\cos \theta d\theta & z>0\\ & =& a^{-2}{[\sin \theta ]}_0^{\alpha }& \alpha ={\tan }^{-1}(z/a)\\ & =& a^{-2}\sin \alpha & \\ & =& a^{-2}\frac{z/a}{\sqrt{1+z^2/a^2}}& =\frac{1}{a^2}\frac{z}{\sqrt{a^2+z^2}}\end{array}$

If the integral is

$I=\underset{0}{\overset{z}{\int }}\sqrt{x^2+a^2}z>0$

then on making this substitution we find

$\begin{array}{cccccc}I& =& a^2\underset{0}{\overset{\alpha }{\int }}{\sec }^3\theta d\theta & & & \alpha ={\tan }^{-1}(z/a)\\ & =& a^2\underset{0}{\overset{\alpha }{\int }}\sec \theta d\tan \theta & & & \\ & =& a^2[\sec \theta \tan \theta {]}_0^{\alpha }& -& a^2\underset{0}{\overset{\alpha }{\int }}\sec \theta {\tan }^2\theta d\theta & \\ & =& a^2\sec \alpha \tan \alpha & -& a^2\underset{0}{\overset{\alpha }{\int }}{\sec }^3\theta d\theta & +a^2\underset{0}{\overset{\alpha }{\int }}\sec \theta d\theta \\ & =& a^2\sec \alpha \tan \alpha & -& I& +a^2\underset{0}{\overset{\alpha }{\int }}\sec \theta d\theta \end{array}$

After integrating by parts, and using trigonometric identities, we've ended up with an expression involving the original integral. In cases like this we must now rearrange the equation so that the original integral is on one side only

$\begin{array}{ccccc}I& =& \frac{1}{2}{a}^2\sec \alpha \tan \alpha & +& \frac{1}{2}{a}^2\underset{0}{\overset{\alpha }{\int }}\sec \theta d\theta \\ & =& \frac{1}{2}{a}^2\sec \alpha \tan \alpha & +& \frac{1}{2}{a}^2{[\ln (\sec \theta +\tan \theta )]}_0^{\alpha }\\ & =& \frac{1}{2}{a}^2\sec \alpha \tan \alpha & +& \frac{1}{2}{a}^2\ln (\sec \alpha +\tan \alpha )\\ & =& \frac{1}{2}{a}^2\left(\sqrt{1+\frac{z^2}{a^2}}\right)\frac{z}{a}& +& \frac{1}{2}{a}^2\ln (\sqrt{1+\frac{z^2}{a^2}}+\frac{z}{a})\\ & =& \frac{1}{2}z\sqrt{z^2+a^2}& +& \frac{1}{2}{a}^2\ln (\frac{z}{a}+\sqrt{1+\frac{z^2}{a^2}})\end{array}$

As we would expect from the integrand, this is approximately z²/2 for large z.

Secant substitution

This substitution is easily derived from a triangle, using the Pythagorean Theorem.

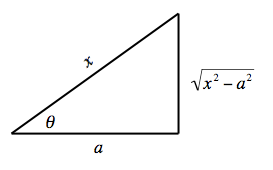
If the integrand contains a factor of the form $\sqrt{x^2-a^2}$ we use the substitution

$x=a\sec \theta dx=a\sec \theta \tan \theta d\theta \sqrt{x^2-a^2}=\tan \theta .$

Example 1

Find $\underset{1}{\overset{z}{\int }}\frac{\sqrt{x^2-1}}{x}dx.$

$\begin{array}{cccc}\underset{1}{\overset{z}{\int }}\frac{\sqrt{x^2-1}}{x}dx& =& \underset{1}{\overset{\alpha }{\int }}\frac{\tan \theta }{\sec \theta }\sec \theta \tan \theta d\theta & z>1\\ & =& \underset{0}{\overset{\alpha }{\int }}{\tan }^2\theta d\theta & \alpha ={\sec }^{-1}z\\ & =& {[\tan \theta -\theta ]}_0^{\alpha }& \tan \alpha =\sqrt{{\sec }^2\alpha -1}\\ & =& \tan \alpha -\alpha & \tan \alpha =\sqrt{z^2-1}\\ & =& \sqrt{z^2-1}-{\sec }^{-1}z& \end{array}$

Example 2

Find $\underset{1}{\overset{z}{\int }}\frac{\sqrt{x^2-1}}{x^2}dx.$

$\begin{array}{cccc}\underset{1}{\overset{z}{\int }}\frac{\sqrt{x^2-1}}{x^2}dx& =& \underset{1}{\overset{\alpha }{\int }}\frac{\tan \theta }{{\sec }^2\theta }\sec \theta \tan \theta d\theta & z>1\\ & =& \underset{0}{\overset{\alpha }{\int }}\frac{{\sin }^2\theta }{\cos \theta }d\theta & \alpha ={\sec }^{-1}z\end{array}$

We can now integrate by parts

$\begin{array}{ccc}\underset{1}{\overset{z}{\int }}\frac{\sqrt{x^2-1}}{x^2}dx& =& -{[\tan \theta \cos \theta ]}_0^{\alpha }+\underset{0}{\overset{\alpha }{\int }}\sec \theta d\theta \\ & =& -\sin \alpha +{[\ln (\sec \theta +\tan \theta )]}_0^{\alpha }\\ & =& \ln (\sec \alpha +\tan \alpha )-\sin \alpha \\ & =& \ln (z+\sqrt{z^2-1})-\frac{\sqrt{z^2-1}}{z}\end{array}$

Trigonometric integrals

Powers of Sine and Cosine

We will give a general method to solve generally integrands of the form cos^m (x)sinⁿ(x). First let us work through an example.

$\int ({\cos }^{3}x)({\sin }^{2}x)dx$

Notice that the integrand contains an odd power of cos. So rewrite it as

$\int ({\cos }^{2}x)({\sin }^{2}x)\cos xdx$

We can solve this by making the substitution u = sin(x) so du = cos(x) dx. Then we can write the whole integrand in terms of u by using the identity

cos(x)² = 1 - sin²(x)=1-u².

So

$\begin{array}{ccc}\int ({\cos }^{3}x)({\sin }^{2}x)dx& =& \int ({\cos }^{2}x)({\sin }^{2}x)\cos xdx\\ & =& \int (1-u^2)u^{2}du\\ & =& \int u^{2}du-\int u^{4}du\\ & =& \frac{1}{3}{u}^3+\frac{1}{5}{u}^5+C\\ & =& \frac{1}{3}{\sin }^{3}x-\frac{1}{5}{\sin }^{5}x+C\end{array}.$

This method works whenever there is an odd power of sine or cosine.

To evaluate $\int ({\cos }^{m}x)({\sin }^{n}x)dx$ when either m or n is odd.

• If m is odd substitute u=sin x and use the identity cos²x = 1 - sin²x=1-u².
• If n is odd substitute u=cos x and use the identity sin²x = 1 - cos²x=1-u².

Example

Find $\underset{0}{\overset{\pi /2}{\int }}{\cos }^{40}(x){\sin }^3(x)dx$.

As there is an odd power of sin we let $u=\cos x$ so du = - sin(x)dx. Notice that when x=0 we have u=cos(0)=1 and when $x=\pi /2$ we have $u=\cos (\pi /2)=0$.

$\begin{array}{ccc}\underset{0}{\overset{\pi /2}{\int }}{\cos }^{40}(x){\sin }^3(x)dx& =& \underset{0}{\overset{\pi /2}{\int }}{\cos }^{40}(x){\sin }^2(x)\sin (x)dx\\ & =& -\underset{1}{\overset{0}{\int }}{u}^{40}(1-u^2)du\\ & =& \underset{0}{\overset{1}{\int }}{u}^{40}(1-u^2)du\\ & =& \underset{0}{\overset{1}{\int }}{u}^{40}-u^{42}du\\ & =& [\frac{1}{41}{u}^{41}-\frac{1}{43}{u}^{43}{]}_0^1\\ & =& \frac{1}{41}-\frac{1}{43}.\end{array}$

When both m and n are even things get a little more complicated.

To evaluate $\int ({\cos }^{m}x)({\sin }^{n}x)dx$ when both m and n are even.

Use the identities sin²x = 1/2 (1- cos 2x) and cos²x = 1/2 (1+ cos 2x).

Example

Find $\int {\sin }^{2}x{\cos }^{4}xdx.$

As sin²x = 1/2 (1- cos 2x) and cos²x = 1/2 (1+ cos 2x) we have

$\int {\sin }^{2}x{\cos }^{4}xdx=\int (\frac{1}{2}(1-\cos 2x)){(\frac{1}{2}(1+\cos 2x))}^{2}dx,$

and expanding, the integrand becomes

$\frac{1}{8}(\int 1-{\cos }^{2}2x+\cos 2x-{\cos }^{3}2xdx).$

Using the multiple angle identities

$\begin{array}{ccc}I& =& \frac{1}{8}(\int 1dx-\int {\cos }^{2}2xdx+\int \cos 2xdx-\int {\cos }^{3}2xdx)\\ & =& \frac{1}{8}(x-\frac{1}{2}\int (1+\cos 4x)dx+\frac{1}{2}\sin 2x-\int {\cos }^{2}2x\cos 2xdx)\\ & =& \frac{1}{16}(x+\sin 2x+\int \cos 4xdx-2\int (1-{\sin }^{2}2x)\cos 2xdx)\end{array}$

then we obtain on evaluating

$I=\frac{x}{16}-\frac{\sin 4x}{64}+\frac{{\sin }^{3}2x}{48}+C$

Powers of Tan and Secant

To evaluate $\int ({\tan }^{m}x)({\sec }^{n}x)dx$.

1. If n is even and $n\ge 2$ then substitute u=tan x and use the identity sec²x = 1 + tan²x.
2. If n and m are both odd then substitute u=sec x and use the identity tan²x = sec²x-1.
3. If n is odd and m is even then use the identity tan²x = sec²x-1 and apply a reduction formula to integrate ${\sec }^{j}xdx.$

Example 1

Find $\int {\sec }^{2}xdx$.

There is an even power of $\sec x$. Substituting $u=\tan x$ gives $du={\sec }^{2}xdx$ so

$\int {\sec }^{2}xdx=\int du=u+C=\tan x+C.$

Example 2

Find $\int \tan xdx$.

Let $u=\cos x$ so $du=-\sin xdx$. Then

$\begin{array}{ccc}\int \tan xdx& =& \int \frac{\sin x}{\cos x}dx\\ & =& \int \frac{-1}{u}du\\ & =& -\ln |u|+C\\ & =& -\ln |\cos x|+C\\ & =& \ln |\sec x|+C.\end{array}$

Example 3

Find $\int \sec xdx$.

The trick to do this is to multiply and divide by the same thing like this:

$\begin{array}{ccc}\int \sec xdx& =& \int \sec x\frac{\sec x+\tan x}{\sec x+\tan x}dx\\ & =& \int \frac{{\sec }^{2}x+\sec x\tan x}{\sec x+\tan x}\end{array}.$

Making the substitution $u=\sec x+\tan x$ so $du=\sec x\tan x+{\sec }^{2}xdx,$

$\begin{array}{ccc}\int \sec xdx& =& \int \frac{1}{u}du\\ & =& \ln |u|+C\\ & =& \ln |\sec x+\tan x|+C\end{array}.$

More trigonometric combinations

For the integrals $\int \sin nx\cos mxdx$ or $\int \sin nx\sin mxdx$ or $\int \cos nx\cos mxdx$ use the identities

• $\sin a\cos b=\frac{1}{2}(\sin (a+b)+\sin (a-b))$
• $\sin a\sin b=\frac{1}{2}(\cos (a-b)-\cos (a+b))$
• $\cos a\cos b=\frac{1}{2}(\cos (a-b)+\cos (a+b))$

Example 1

Find $\int \sin 3x\cos 5xdx.$

We can use the fact that sin a cos b=(1/2)(sin(a+b)+sin(a-b)), so

$\sin 3x\cos 5x=(\sin 8x+\sin (-2x))/2$

Now use the oddness property of sin(x) to simplify

$\sin 3x\cos 5x=(\sin 8x-\sin 2x)/2$

And now we can integrate

$\begin{array}{ccc}\int \sin 3x\cos 5xdx& =& \frac{1}{2}\int \sin 8x-\sin 2xdx\\ & =& \frac{1}{2}(-\frac{1}{8}\cos 8x+\frac{1}{2}\cos 2x)+C\end{array}$

Example 2

Find:$\int \sin x\sin 2xdx$.

Using the identities

$\sin x\sin 2x=\frac{1}{2}(\cos (-x)-\cos (3x))=\frac{1}{2}(\cos x-\cos 3x).$

Then

$\begin{array}{ccc}\int \sin x\sin 2xdx& =& \frac{1}{2}\int (\cos x-\cos 3x)dx\\ & =& \frac{1}{2}(\sin x-\frac{1}{3}\sin 3x)+C\end{array}$

Reduction formula

A reduction formula is one that enables us to solve an integral problem by reducing it to a problem of solving an easier integral problem, and then reducing that to the problem of solving an easier problem, and so on.

For example, if we let

$I_n=\int x^n{e}^{x}dx$

Integration by parts allows us to simplify this to

$I_n=x^n{e}^x-n\int x^{n-1}{e}^{x}dx=$

$I_n=x^n{e}^x-n{I}_{n-1}$

which is our desired reduction formula. Note that we stop at

$I_0=e^x$.

Similarly, if we let

$I_n=\underset{0}{\overset{\alpha }{\int }}{\sec }^n\theta d\theta$

then integration by parts lets us simplify this to

$I_n={\sec }^{n-2}\alpha \tan \alpha -(n-2)\underset{0}{\overset{\alpha }{\int }}{\sec }^{n-2}\theta {\tan }^2\theta d\theta$

Using the trigonometric identity, tan²=sec²-1, we can now write

$\begin{array}{cccc}{I}_n& =& {\sec }^{n-2}\alpha \tan \alpha & +(n-2)(\underset{0}{\overset{\alpha }{\int }}{\sec }^{n-2}\theta d\theta -\underset{0}{\overset{\alpha }{\int }}{\sec }^n\theta d\theta )\\ & =& {\sec }^{n-2}\alpha \tan \alpha & +(n-2)(I_{n-2}-I_n)\end{array}$

Rearranging, we get

$I_n=\frac{1}{n-1}{\sec }^{n-2}\alpha \tan \alpha +\frac{n-2}{n-1}{I}_{n-2}$

Note that we stop at n=1 or 2 if n is odd or even respectively.

As in these two examples, integrating by parts when the integrand contains a power often results in a reduction formula.

Rational functions in Sine and Cosine

The "tan half angle" substitution

Another useful change of variables is

$t=\tan (x/2)$

With this transformation, using the double-angle trig identities,

$\sin x=\frac{2t}{1+t^2}\cos x=\frac{1-t^2}{1+t^2}\tan x=\frac{2t}{1-t^2}dx=\frac{2dt}{1+t^2}$

This transforms a trigonometric integral into a algebraic integral, which may be easier to integrate.

For example, if the integrand is 1/(1 + sin x ) then

$\begin{array}{ccc}\underset{0}{\overset{\pi /2}{\int }}\frac{dx}{1+\sin x}& =& \underset{0}{\overset{1}{\int }}\frac{2dt}{(1+t{)}^2}\\ & =& {[-\frac{2}{1+t}]}_0^1\\ & =& 1\end{array}$

This method can be used to further simplify trigonometric integrals produced by the changes of variables described earlier.

For example, if we are considering the integral

$I=\underset{-1}{\overset{1}{\int }}\frac{\sqrt{1-x^2}}{1+x^2}dx$

we can first use the substition x= sin θ, which gives

$I=\underset{-\pi /2}{\overset{\pi /2}{\int }}\frac{{\cos }^2\theta }{1+{\sin }^2\theta }d\theta$

then use the tan-half-angle substition to obtain

$I=\underset{-1}{\overset{1}{\int }}\frac{(1-t^2{)}^2}{1+6t^2+t^4}\frac{2dt}{1+t^2}$

In effect, we've removed the square root from the original integrand. We could do this with a single change of variables, but doing it in two steps gives us the opportunity of doing the trigonometric integral another way.

Having done this, we can split the new integrand into partial fractions, and integrate.

$\begin{array}{ccc}I& =& \underset{-1}{\overset{1}{\int }}\frac{2-\sqrt{2}}{t^2+3-\sqrt{8}}dt+\underset{-1}{\overset{1}{\int }}\frac{2+\sqrt{2}}{t^2+3+\sqrt{8}}dt-\underset{-1}{\overset{1}{\int }}\frac{2}{1+t^2}dt\\ & =& \frac{4-\sqrt{8}}{\sqrt{3-\sqrt{8}}}{\tan }^{-1}(\sqrt{3+\sqrt{8}})+\frac{4+\sqrt{8}}{\sqrt{3+\sqrt{8}}}{\tan }^{-1}(\sqrt{3-\sqrt{8}})-\pi \end{array}$

This result can be further simplified by use of the identities

$3\pm \sqrt{8}={(\sqrt{2}\pm 1)}^2\tan (\sqrt{2}\pm 1)=(\frac{1}{4}\pm \frac{1}{8})\pi$

ultimately leading to

$I=(\sqrt{2}-1)\pi$

In principle, this approach will work with any integrand which is the square root of a quadratic multiplied by the ratio of two polynomials. However, it should not be applied automatically.

E.g, in this last example, once we deduced

$I=\underset{-\pi /2}{\overset{\pi /2}{\int }}\frac{{\cos }^2\theta }{1+{\sin }^2\theta }d\theta$

we could have used the double angle formulae, since this contains only even powers of cos and sin. Doing that gives

$I=\underset{-\pi /2}{\overset{\pi /2}{\int }}\frac{1+\cos 2\theta }{3-\cos 2\theta }d\theta =\frac{1}{2}\underset{-\pi }{\overset{\pi }{\int }}\frac{1+\cos \varphi }{3-\cos \varphi }d\varphi$

Using tan-half-angle on this new, simpler, integrand gives

$\begin{array}{ccc}I& =& \underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\frac{1}{1+2t^2}\frac{dt}{1+t^2}\\ & =& \underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\frac{2dt}{1+2t^2}-\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\frac{dt}{1+t^2}\end{array}$

This can be integrated on sight to give

$I=\frac{4}{\sqrt{2}}\frac{\pi }{2}-2\frac{\pi }{2}=(\sqrt{2}-1)\pi$

This is the same result as before, but obtained with less algebra, which shows why it is best to look for the most straightforward methods at every stage.

A more direct way of evaluating the integral I is to substitute t = tan θ right from the start, which will directly bring us to the line

$I=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\frac{1}{1+2t^2}\frac{dt}{1+t^2}$

above. More generally, the substitution t = tan x gives us

$\sin x=\frac{t}{\sqrt{1+t^2}}\cos x=\frac{1}{\sqrt{1+t^2}}dx=\frac{dt}{1+t^2}$

so this substitution is the preferable one to use if the integrand is such that all the square roots would disappear after substitution, as is the case in the above integral.

Alternate Method

In general, to evaluate integrals of the form

$\int \frac{A+B\cos x+C\sin x}{a+b\cos x+c\sin x}dx$,

it is extremely tedious to use the aforementioned "tan half angle" substitution directly, as one easily ends up with a rational function with a 4th degree denominator. Instead, we may first write the numerator as

$A+B\cos x+C\sin x\equiv p(a+b\cos x+c\sin x)+q\frac{d}{dx}(a+b\cos x+c\sin x)+r$.

Then the integral can be written as

$\int (p+\frac{q\frac{d}{dx}(a+b\cos x+c\sin x)}{a+b\cos x+c\sin x}+\frac{r}{a+b\cos x+c\sin x})dx$

which can be evaluated much more easily.

Example

Evaluate $\int \frac{\cos x+2}{\cos x+\sin x}dx$.

Let

$\cos x+2\equiv p(\cos x+\sin x)+q\frac{d}{dx}(\cos x+\sin x)+r$.

Then

$\cos x+2\equiv p(\cos x+\sin x)+q(-\sin x+\cos x)+r$

$\cos x+2\equiv (p+q)\cos x+(p-q)\sin x+r$.

Comparing coefficients of cos x, sin x and the constants on both sides, we obtain

$\{\begin{array}{ccc}p+q& =& 1\\ p-q& =& 0\\ r& =& 2\end{array}$

yielding p = q = 1/2, r = 2. Substituting back into the integrand,

$\int \frac{\cos x+2}{\cos x+\sin x}dx=\int \frac{1}{2}dx+\frac{1}{2}\int \frac{d(\cos x+\sin x)}{\cos x+\sin x}+\int \frac{2}{\cos x+\sin x}dx$.

The last integral can now be evaluated using the "tan half angle" substitution described above, and we obtain

$\int \frac{2}{\cos x+\sin x}dx=\sqrt{2}\ln \left|\frac{\tan \frac{x}{2}-1+\sqrt{2}}{\tan \frac{x}{2}-1-\sqrt{2}}\right|+C$.

The original integral is thus

$\int \frac{\cos x+2}{\cos x+\sin x}dx=\frac{x}{2}+\frac{1}{2}\ln |\cos x+\sin x|+\sqrt{2}\ln \left|\frac{\tan \frac{x}{2}-1+\sqrt{2}}{\tan \frac{x}{2}-1-\sqrt{2}}\right|+C$.

Irrational functions

Integration of irrational functions is more difficult than rational functions, and many cannot be done. However, there are some particular types that can be reduced to rational forms by suitable substitutions.

Type 1

Integrand contains $\sqrt[n]{\frac{ax+b}{cx+d}}$

Use the substitution $u=\sqrt[n]{\frac{ax+b}{cx+d}}$.

Example

Find $\int \frac{1}{x}\sqrt{\frac{1-x}{x}}dx$.

Type 2

Integral is of the form $\int \frac{Px+Q}{\sqrt{a{x}^2+bx+c}}dx$

Write $Px+Q$ as $Px+Q=p\frac{d}{dx}(a{x}^2+bx+c)+q$.

Example

Find $\int \frac{4x-1}{\sqrt{5-4x-x^2}}dx$.

Type 3

Integrand contains $\sqrt{a^2-x^2}$, $\sqrt{a^2+x^2}$ or $\sqrt{x^2-a^2}$

This was discussed in "trigonometric substitutions above". Here is a summary:

1. For $\sqrt{a^2-x^2}$, use $x=a\sin \theta$.
2. For $\sqrt{a^2+x^2}$, use $x=a\tan \theta$.
3. For $\sqrt{x^2-a^2}$, use $x=a\sec \theta$.

Type 4

Integral is of the form $\int \frac{1}{(px+q)\sqrt{a{x}^2+bx+c}}dx$

Use the substitution $u=\frac{1}{px+q}$.

Example

Find $\int \frac{1}{(1+x)\sqrt{3+6x+x^2}}dx$.

Type 5

Other rational expressions with the irrational function $\sqrt{a{x}^2+bx+c}$

1. If $a>0$, we can use $u=\sqrt{a{x}^2+bx+c}\pm \sqrt{a}x$.
2. If $c>0$, we can use $u=\frac{\sqrt{a{x}^2+bx+c}\pm \sqrt{c}}{x}$.
3. If $a{x}^2+bx+c$ can be factorised as $a(x-\alpha )(x-\beta )$, we can use $u=\sqrt{\frac{a(x-\alpha )}{x-\beta }}$.
4. If $a<0$ and $a{x}^2+bx+c$ can be factorised as $-a(\alpha -x)(x-\beta )$, we can use $x=\alpha {\cos }^2\theta +\beta {\sin }^2\theta$,$/theta+\beta .$