Trigonometry/Radian and degree measures
A Definition and Terminology of Angles
An angle is determined by rotating a ray about its endpoint. The starting position of the ray is called the initial side of the angle. The ending position of the ray is called the terminal side. The endpoint of the ray is called its vertex. Positive angles are generated by counter-clockwise rotation. Negative angles are generated by clockwise rotation. Consequently an angle has four parts: its vertex, its initial side, its terminal side, and its rotation.
An angle is said to be in standard position when it is drawn in a cartesian coordinate system in such a way that its vertex is at the origin and its initial side is the positive x-axis.

The radian measure
One way to measure angles is in radians. To signify that a given angle is in radians, a superscript c, or the abbreviation rad might be used. If no unit is given on an angle measure, the angle is assumed to be in radians.
Template:TrigBoxOpen Template:TrigBoxClose
Defining a radian
A single radian is defined as the angle formed in the minor sector of a circle, where the minor arc length is the same as the radius of the circle.
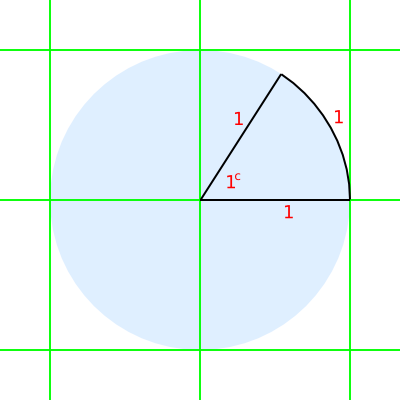
Measuring an angle in radians
The size of an angle, in radians, is the length of the circle arc s divided by the circle radius r.

We know the circumference of a circle to be equal to , and it follows that a central angle of one full counterclockwise revolution gives an arc length (or circumference) of . Thus 2 π radians corresponds to 360°, that is, there are radians in a circle.
Converting from Radians to Degrees
Because there are 2π radians in a circle:
To convert degrees to radians:
To convert radians to degrees:
Exercises
Exercise 1:Degree-Radian Conversion
| A) Convert 180° into radian measure. |
|---|
| B) Convert 90° into radian measure. |
|---|
| C) Convert 45° into radian measure. |
|---|
| D) Convert 137° into radian measure. |
|---|
Exercise 2: Radian-Degree Conversion
Convert the following angle measurements from radians to degrees.
| A) Convert into degree measure. |
|---|
| 60° |
| B) Convert into degree measure. |
|---|
| 30° |
| C) Convert into degree measure. |
|---|
| 420° |
| D) Convert into degree measure. |
|---|
| 135° |
Next Page: The Unit Circle
Previous Page: In Simple Terms
Home: Trigonometry